

Radiation Quantities and Units
Perry Sprawls, Ph.D.
Introduction and Overview
Several forms of ionizing radiation are used in medical imaging. Even though
the risk is low, if there is a risk at all, it is appropriate to manage the
radiation delivered to patients being imaged and to use only sufficient
radiation to produce the necessary image quality. The question we begin with is:
How much radiation is delivered to a patient's body?
 As we are about to see, that is
not always an easy question to answer. There are several factors contributing to
the complexity. They include the many quantities that can be used to express the
amount of radiation, the different units that are used, and the generally uneven
distribution of the radiation within the patients body.
As we are about to see, that is
not always an easy question to answer. There are several factors contributing to
the complexity. They include the many quantities that can be used to express the
amount of radiation, the different units that are used, and the generally uneven
distribution of the radiation within the patients body.
Also, some medical imaging procedures expose the staff to radiation. It is necessary to determine their exposure so that the risk can be managed in the context of ALARA programs.
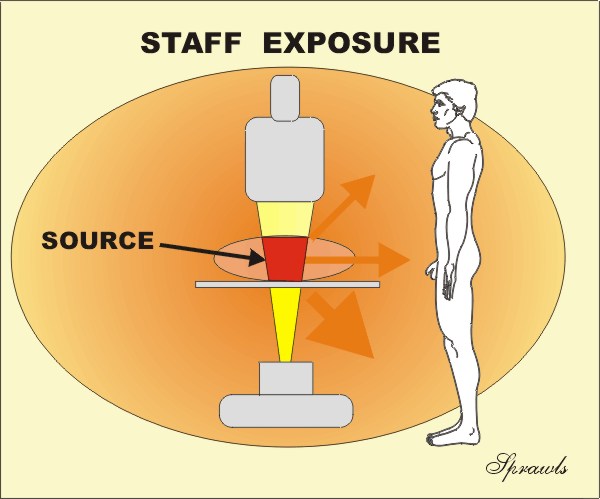
Determining and expressing the radiation to the staff and other persons in an imaging facility is also somewhat complex because of the reasons mentioned above.
Radiation Quantities
As we see below, there are many
different physical quantities that can be used to express the amount of
radiation delivered to a human body. Generally, there are both advantages and
applications as well as disadvantages and limitations for each of the
quantities.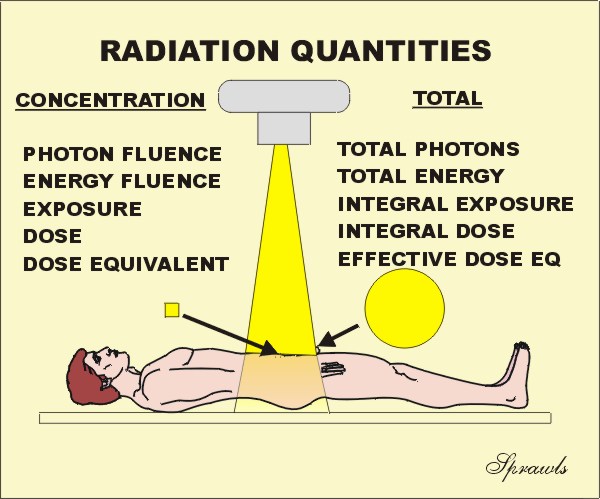 There are two types of radiation
quantities: those that express the
concentration of radiation at some
point, or to a specific tissue or organ, and there are also quantities that
express the total radiation
delivered to a body. We will be considering each of these quantities in much
more detail.
There are two types of radiation
quantities: those that express the
concentration of radiation at some
point, or to a specific tissue or organ, and there are also quantities that
express the total radiation
delivered to a body. We will be considering each of these quantities in much
more detail.
The general relationship between the concentration and total radiation quantities are illustrated below.
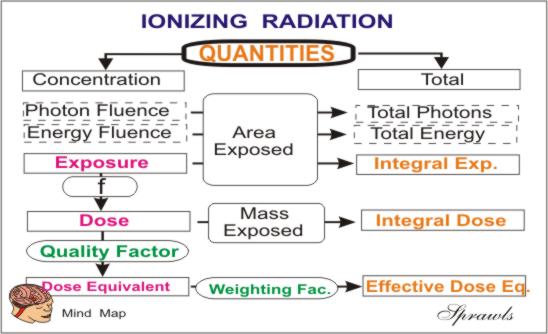
Radiation Units
Throughout the course of history there have been
many different systems of units developed to express the values of the various
physical quantities. In more recent times the metric system has gradually
replaced some of the other more traditional or classic systems. This is
also true for the units used for many of our radiation quantities.
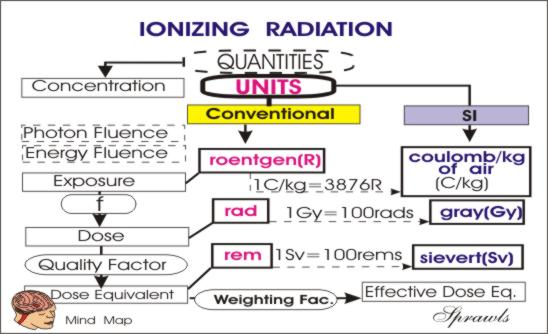
Conventional Units
During the relatively short era (just over one
century) of medical applications of ionizing radiation, a variety of radiation
units were developed. We will refer to these as the conventional units.
These are such units as the "three Rs", the roentgen, rad, and rem. All of these
were very practical units and have served their purpose well. However,
they did not fit into the metric system of units, specifically the
Système International
d'unités (SI units) that is being promoted for the sake of having one unified
system of units for all physical quantities.
SI Units
The SI
radiation units have been adopted by most organizations and publications.
However, because of their practicality and familiarity, some of the conventional
units, especially the roentgen, will continue to be used by many.
With respect to the two systems of units, we are faced with the necessity of recognizing and understanding the different units, and make conversions between the two systems when necessary.
Specific Quantities and
Their Associated Units
We will now consider each of the radiation quantities and their associated units in detail.
As an overview, they are listed below showing if there are concentration or
total radiation quantities.
NOTE: You can jump to the discussion of any quantity by
clicking on it's name below.
|
Radiation Concentration |
Total Radiation |
|
Air Kerma |
|
Photons
Let us recall that all forms of electromagnetic
radiation (light, x-ray, gamma, etc) are actually packaged and delivered in the
form of many many small units of energy, the photons. As we have already
discovered in a previous module, the physical difference between the different
types of radiation, like light and x-rays, is the amount of energy packaged in
each photon. Therefore, it is logical to consider expressing the amount of
radiation delivered to an object, such as a human body, in terms of either the
total number or the concentration of the photons.
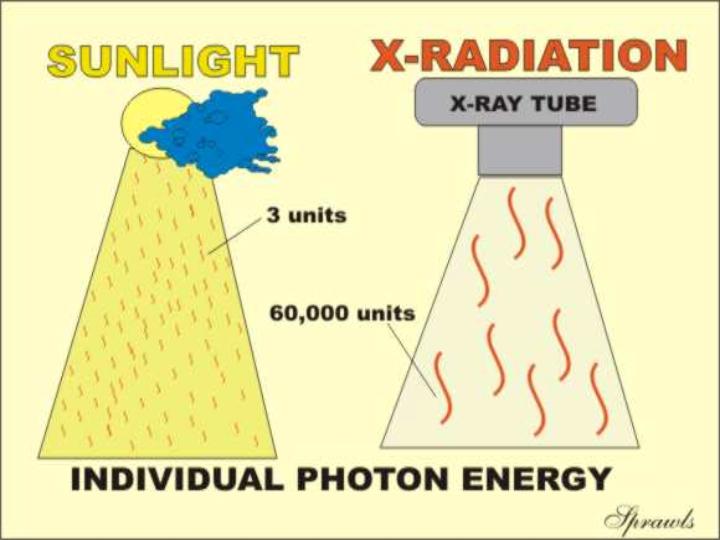 This
turns out to not be the most practical approach. There are several
reasons. One is that the number of photons in a typical x-ray beam is such
a large number, like in the billions or more, that it is not a practical
quantity to work with. Another reason is that, especially in x-ray beams,
we do not have practical instruments for counting those large quantity of
photons. As we will see, it is more practical to measure some other
quantities that we will meet later.
This
turns out to not be the most practical approach. There are several
reasons. One is that the number of photons in a typical x-ray beam is such
a large number, like in the billions or more, that it is not a practical
quantity to work with. Another reason is that, especially in x-ray beams,
we do not have practical instruments for counting those large quantity of
photons. As we will see, it is more practical to measure some other
quantities that we will meet later.
It is very helpful to our understanding of radiation to see it as a shower of photons, even if we do not usually quantify the radiation in that manner. However, in medical imaging there are two situations in which we are concerned with the number of protons.
Total Photons,
A Measure of Radioactivity
One
method used to measure the radioactivity of a sample is to count the photons
that are emitted. Then, with proper calibration factors, the counts per
minute (CPM) can be converted into units of radioactivity, curies or becquerels.
Photon Concentration (Fluence),
A
Factor in Image Quality
In all forms of medical imaging using ionization
radiation (x-ray, gamma, etc) the concentration of photons absorbed in the
image forming process is a very critical factor. As described in another
module, this is the principle factor that determines the amount of visual
noise in the image. That is the so-called quantum (photon) noise.
As we will learn later, the image noise is decreased by increasing the
photon concentration. In projection imaging (radiography,
fluoroscopy, gamma camera) the critical quantity is the concentration
(photons/unit area) absorbed by the image receptor that determines the
noise level.
In CT, it is the concentration of photons absorbed in each tissue voxel
that determines the noise.
So, photon concentration (fluence) is an important factor in producing
good quality images.
Energy
The radiation used for all types of medical imaging deposits
energy in the patient's body. This happens when the radiation (which is
energy) interacts with and is absorbed by the tissues. Since energy is one
of the fundamental physical quantities, it is logical that this would be an
appropriate quantity for expressing the amount of radiation delivered to a body.
This is done, but the quantity is usually not called energy. As we are
about to see, the concentration of energy absorbed in tissue is the quantity,
Absorbed
Dose , and the total energy absorbed in a body is the
Integral
Dose . We will come back to these quantities later, but it
is appropriate to consider some other quantities before we do.
Exposure
Exposure
is a radiation quantity that
expresses the concentration of radiation delivered to a specific point,
such as the surface of the human body.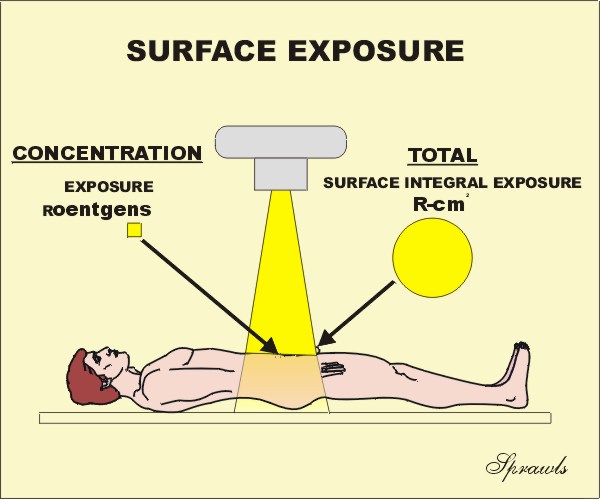 We
need to emphasize that this expresses only the concentration at some specified
point. Knowing the exposure tells us nothing about the total radiation imparted
to a body. This can be expressed by several quantities, the first that we
will consider is the
Surface Integral Exposure (SIE) . We
will come back to this after developing more of the details of the quantity,
Exposure
.
We
need to emphasize that this expresses only the concentration at some specified
point. Knowing the exposure tells us nothing about the total radiation imparted
to a body. This can be expressed by several quantities, the first that we
will consider is the
Surface Integral Exposure (SIE) . We
will come back to this after developing more of the details of the quantity,
Exposure
.
There are two units for expressing Exposure. The conventional unit is the roentgen (R) and the SI unit is the coulomb/kg of air (C/kg of air). Now lets find out where these units cam from and their relationship. It goes back to the early days of x-radiation when it was discovered that one of the effects of radiation was that it ionized air. As it turned out, this was a very practical way of detecting and measuring radiation. The procedure is to expose a small volume of air contained in an ionization chamber to the radiation and then measure the amount of ionization that was produced in the air. This is relatively easy to do because the ionization affects the electrical conductivity of the air and can be measured with an electrometer. Because of this method of measurement, the unit, the roentgen, is officially defined in terms of the amount of ionization produced in a specific quantity of air. The ionization process produces an electrical charge that is expressed in the unit of coulombs. So, by measuring the amount of ionization (in coulombs) in a known quantity of air the exposure in roentgens can be determined. The relationship is:
|
|
Most of us do not need to get involved
with this relationship because most ionization chamber instruments are
calibrated to readout directly in roentgens.
Now a question, what is wrong with the roentgen as a unit for expressing
exposure? My opinion is that there is not anything wrong with it. It
is a great unit that is well established and very practical. It is just
about the right size for expressing exposure values encountered in medical
imaging and it has a very convenient relationship to absorbed dose in rads for
most soft tissues. It also honors the physicist who gave birth to medical
imaging.
The opposition to the roentgen as a unit is that it is not a whole number, it is
a fraction of a C/kg of air.
The SI unit for exposure is the C/kg of air.
This is a very awkward unit and not very practical but it is "pure" and fits into the SI scheme.
From time to time we might find it necessary to convert between the two units. The conversion is:
|
|
The usual and appropriate use of the quantity, exposure, is to express the concentration of radiation delivered to a specific point, such as the Entrance Surface Exposure for a patient. Although knowing the surface entrance exposure to a patient does not give a complete description of the radiation delivered to all tissues, it does provide useful information for several purposes. Entrance Surface Exposure values can be used to:
Compare different imaging techniques with respect to radiation delivered to patients, especially for the same anatomical coverage.
Calculate the absorbed dose to underlying tissues and organs.
Air
kerma
Air kerma is another radiation quantity that is sometimes
used to express the radiation concentration delivered to a point, such as the
entrance surface of a patient's body. It is a quantity that fits into the
SI scheme.
The quantity, kerma, originated from the acronym, KERMA, for Kinetic
Energy Released per unit MAss (of air). It is a measure of the amount of
radiation energy, in the unit of joules (J), actually deposited in or absorbed
in a unit mass (kg) of air. Therefore, the quantity, kerma, is expressed
in the units of J/kg which is also the radiation unit, the gray (G) . A
little later we are going to discover that the concentration of radiation energy
absorbed in a material is actually the radiation quantity,
Absorbed Dose , but more on that later. At this time we just need
to recognize that air kerma is just the
Absorbed Dose
in air.
The quantity, air kerma, has two things going for
it and is beginning to replace the quantity, exposure, for expressing the
concentration of radiation delivered to a point, like the entrance surface to a
human body (patient or staff).
1. It is
easy to measure with an ionization chamber. Since the
ionization produced in air by radiation is proportional to the energy released
in the air by the radiation, ionization chambers actually measure air kerma as
well as exposure. An ionization chamber can be calibrated to read air
kerma, or a conversion factor can be used to convert between air kerma and
exposure values.
2. It is expressed in a practical metric SI unit. Air kerma (energy released in a unit mass of air) is expressed in the units of joule per kilogram, J/kg. This is also the unit gray, Gy, used for absorbed dose. Here is the easy part. If we know air kerma measured (or calculated) at a point where soft tissue is located, the absorbed dose in the tissue will be just about equal to the air kerma.
Up to this point, we have been considering quantities and units that can be used to express the concentration of radiation delivered to some location, such as the surface of a body. The four quantities were: energy fluence, photon fluence, exposure, and air kerma. While each of these quantities have useful applications, they are very limited in that they do not give information on the total radiation delivered to a body. For that we now turn to several other quantities.
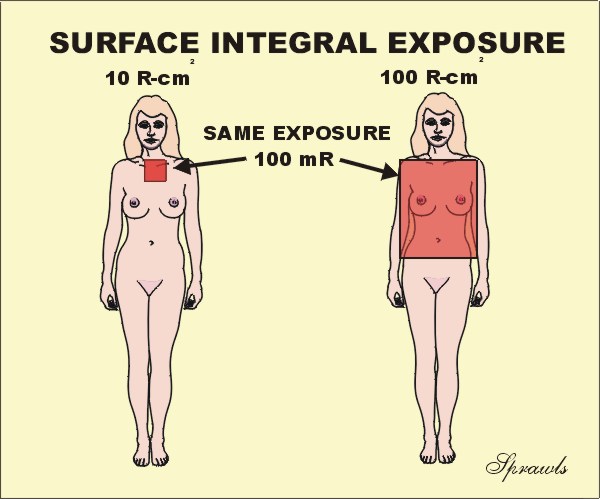 The
first is the Surface Integral Exposure (SIE) that is illustrated here. The
concept is simple. If we have a uniform exposure over some area of a body,
then the SIE is just the product of the exposure value (mR) and the size of the
exposed area (cm2). The unit for SIE is
the R-cm2. Note: it is not R/cm2, it is the
product. An alternate name that is sometimes used for this quantity is
Exposure Area Product. When the exposure is not uniformly distributed over
the exposed area , like in the fluoroscopic example coming up, the SIE is
the sum (or integral) of the individual area and exposure products for the
entire body. The value of the SIE compared to just surface entrance
exposure, is that it gives information about the total radiation (not just
concentration) delivered to a body. Generally, the risk of the stochastic
effect, cancer induction, is probably related, to some degree, to the total
radiation to a body. Consider the two patients shown here. Both received
the same exposure, 100mR. But did they both receive the same amount of
radiation? The exposure to the lady on the right was to a much larger area
of her body. She received an SIE of 100 R-cm2 compared to only 10
R-cm2 for the lady on the left. Here is a good example of
where just knowing the exposure (100 mR), dose not tell the full story.
The
first is the Surface Integral Exposure (SIE) that is illustrated here. The
concept is simple. If we have a uniform exposure over some area of a body,
then the SIE is just the product of the exposure value (mR) and the size of the
exposed area (cm2). The unit for SIE is
the R-cm2. Note: it is not R/cm2, it is the
product. An alternate name that is sometimes used for this quantity is
Exposure Area Product. When the exposure is not uniformly distributed over
the exposed area , like in the fluoroscopic example coming up, the SIE is
the sum (or integral) of the individual area and exposure products for the
entire body. The value of the SIE compared to just surface entrance
exposure, is that it gives information about the total radiation (not just
concentration) delivered to a body. Generally, the risk of the stochastic
effect, cancer induction, is probably related, to some degree, to the total
radiation to a body. Consider the two patients shown here. Both received
the same exposure, 100mR. But did they both receive the same amount of
radiation? The exposure to the lady on the right was to a much larger area
of her body. She received an SIE of 100 R-cm2 compared to only 10
R-cm2 for the lady on the left. Here is a good example of
where just knowing the exposure (100 mR), dose not tell the full story.
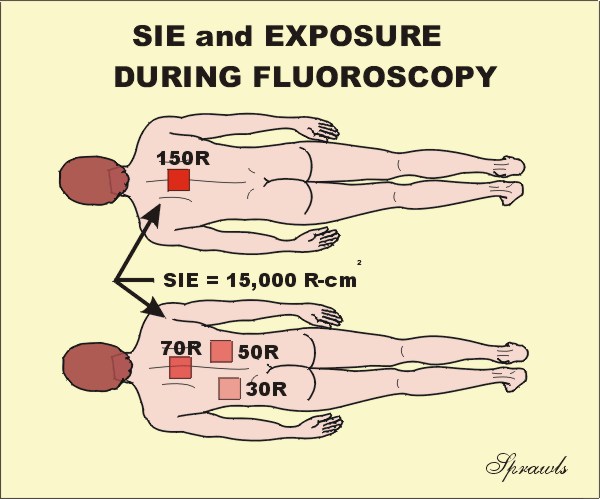 Fluoroscopy
provides another good application to compare the use of SIE and Exposure. Let's
consider these two patients. Both received the same SIE, 15,000 R-cm2
because the fluoroscopic time was the same. Now the question is, did they
receive the same surface exposure? The difference is that for the upper
patient, the x-ray beam was not moved during the procedure and all of the
radiation was concentrated in one area. This produced a relatively high exposure
of 150 R to that area. During the procedure for the lower patient, the beam was
moved to several different areas. This distributed the radiation so it was
not all concentrated in one area. So, which quantity, exposure or SIE,
provided the most information? It depends on what type of risk is being
considered. The stochastic risk of cancer is probably more related to the
SIE. The risk of skin burning is more related to exposure, that is the
concentration of the radiation.
Fluoroscopy
provides another good application to compare the use of SIE and Exposure. Let's
consider these two patients. Both received the same SIE, 15,000 R-cm2
because the fluoroscopic time was the same. Now the question is, did they
receive the same surface exposure? The difference is that for the upper
patient, the x-ray beam was not moved during the procedure and all of the
radiation was concentrated in one area. This produced a relatively high exposure
of 150 R to that area. During the procedure for the lower patient, the beam was
moved to several different areas. This distributed the radiation so it was
not all concentrated in one area. So, which quantity, exposure or SIE,
provided the most information? It depends on what type of risk is being
considered. The stochastic risk of cancer is probably more related to the
SIE. The risk of skin burning is more related to exposure, that is the
concentration of the radiation.
Dose Area Product
Dose Area Product (DAP) is similar in concept to surface integral
exposure and exposure area product in that they all express total radiation
delivered to a patient. The principle difference is in the units used.
DAP is in dose units, such as Gy-cm2. For a uniformly exposed
area, the DAP is just the product of the air kerma ,in Gy or mGy, and the
exposed area in cm2. DAP provides a good estimation of the total
radiation energy delivered to a patient during a procedure.
Both radiographic and fluoroscopic machines can be equipped with devices (DAP meters) or computer programs that measure or calculate the DAP for each procedure. It is the most practical quantity for monitoring the radiation delivered to patients.
Absorbed Dose
Absorbed Dose is the radiation quantity used to express the
concentration of radiation energy actually absorbed in a specific tissue.
This is the quantity that is most directly related to biological effects.
Dose values can be in the traditional unit of the rad or the SI unit of the gray
(Gy). The rad is equivalent to 100 ergs of energy absorbed in a gram of
tissue and the gray is one joule of energy absorbed per kilogram of tissue.
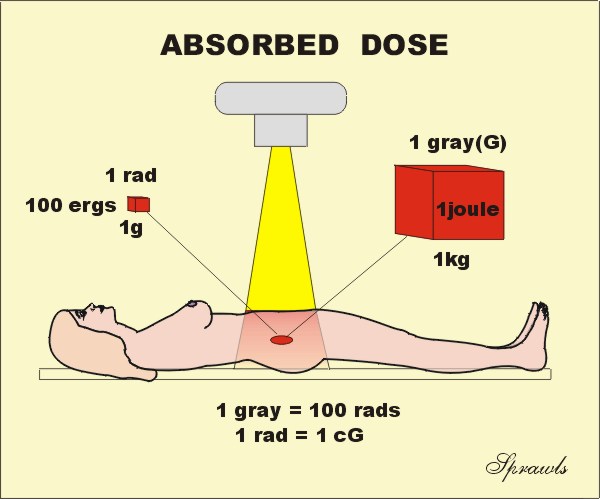 The
conversion between the two units is easy (if you get the decimal point
correct!).
The
conversion between the two units is easy (if you get the decimal point
correct!).
|
|
The quantities relating to radiation outside of a human body, such as exposure, air kerma, SIE, and DAP, are relatively easy to measure because a measuring devise, ionization chamber or DAP meter, can be placed at the location of interest. However, absorbed dose in tissue cannot be measured directly by any practical methods. Dose measuring devices, dosimeters, can be placed on the surface, but it is generally not reasonable to insert them into most internal tissues or organs. The absorbed dose in most body tissues is usually determined by indirect means.
A common method is to first determine the entrance surface exposure, or air kerma, over the tissue or organ of interest and then use published dose factors to calculate the dose in a specific tissue location. The dose to the breast tissue in mammography is determined by this method and will be discussed more later.
Another method used to determine dose is to actually measure the dose in a "phantom". A phantom is a block of some material (usually plastic or water) that has the same radiation absorption properties as tissue. The phantom should be approximately the same size and shape as the body section in which the dose is to be determined. A dosimeter is inserted into the phantom and it is then exposed to radiation using known exposure factors. These measured dose values in the phantom can them be used to estimate patient dose values by applying appropriate factors to account for different exposure conditions.
It is not always easy to determine the absorbed dose to a specific tissue location or organ in a patient undergoing an imaging procedure. There are several complicating factors, including variations in organ size and location, variations in body size and composition, and the non-uniformity of the radiation distribution within the body. To overcome some of these difficulties several special radiation dose quantities have been developed for specific imaging procedures, such as CT and mammography. These special quantities make it possible to determine a dose value that is a reasonable estimate of the "true dose" that is actually delivered to the tissue. These special dose quantities are usually determined by following well established measurement and calculation protocols. This makes it possible to compare dose values for different imaging techniques, among institutions, and from country to country. We will now look at tow of these special quantities.
Computed Tomography Dose
Index
The Computed Tomography Dose Index, CTDI, is the
special dose quantity that is used extensively to express absorbed dose in CT.
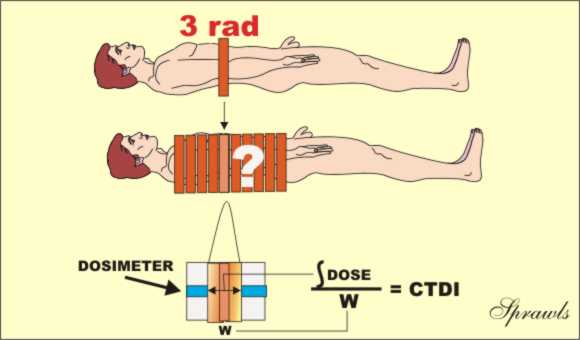 Let's
recall that in CT the x-ray beam is rotated around the patient and passes
through from all sides. This gives a relatively uniform distribution of absorbed
dose within each slice. A dose value determined at the center of the slice
is usually considered a good indicator of tissue dose and can be used to compare
imaging techniques and for dose management purposes. One of the
complicating factors in determining CT dose is that the tissue in a slice is
exposed to two sources of x-radiation. One is the direct beam and the
other is the scattered radiation from adjacent slices in the typical multiple
slice imaging procedure. It is the contribution from the scattered radiation
that is very difficult to measure. Values for the CTDI are determined by a
measuring protocol that makes a reasonable estimate of the dose contribution
from scatter. The typical procedure is illustrated above. A pencil
shaped dosimeter (ionization chamber) is placed in a phantom. It is then
scanned for only one complete slice and the dose value is read. The
dosimeter will read the radiation from the direct x-ray beam within the
slice plus the scattered radiation coming out of the sides of the slice
and reaching the dosimeter. Here is a somewhat subtle but crucial point:
the concept of the CTDI is based on the assumption that the scatter measured
from a single slice, as just described, is a good estimate of the scatter into a
slice from adjacent slices in a multiple-slice scan. This procedure does
provide a good approximation of the actual dose, but since it is not completely
precise, it is called a dose index.
Let's
recall that in CT the x-ray beam is rotated around the patient and passes
through from all sides. This gives a relatively uniform distribution of absorbed
dose within each slice. A dose value determined at the center of the slice
is usually considered a good indicator of tissue dose and can be used to compare
imaging techniques and for dose management purposes. One of the
complicating factors in determining CT dose is that the tissue in a slice is
exposed to two sources of x-radiation. One is the direct beam and the
other is the scattered radiation from adjacent slices in the typical multiple
slice imaging procedure. It is the contribution from the scattered radiation
that is very difficult to measure. Values for the CTDI are determined by a
measuring protocol that makes a reasonable estimate of the dose contribution
from scatter. The typical procedure is illustrated above. A pencil
shaped dosimeter (ionization chamber) is placed in a phantom. It is then
scanned for only one complete slice and the dose value is read. The
dosimeter will read the radiation from the direct x-ray beam within the
slice plus the scattered radiation coming out of the sides of the slice
and reaching the dosimeter. Here is a somewhat subtle but crucial point:
the concept of the CTDI is based on the assumption that the scatter measured
from a single slice, as just described, is a good estimate of the scatter into a
slice from adjacent slices in a multiple-slice scan. This procedure does
provide a good approximation of the actual dose, but since it is not completely
precise, it is called a dose index.
The CTDI can be measured at points other than the center of a slice, if that
information is needed.
Mammography Mean Glandular Dose
The Mean Glandular Dose (MGD) is the special dose quantity used
in mammography. It is defined as the mean, or average, dose to the
glandular tissue within the breast. The assumption is that the glandular
tissue, and not the fat, is the tissue at risk from radiation exposure.
Obviously, it is just about impossible to determine the actual dose to the
glandular tissue during a specific mammographic procedure because of variations
in breast size and distribution of glandular tissue within the breast. The
MGD is based on some standard breast parameters.
MGD values are determined by following a standard two-step protocol.
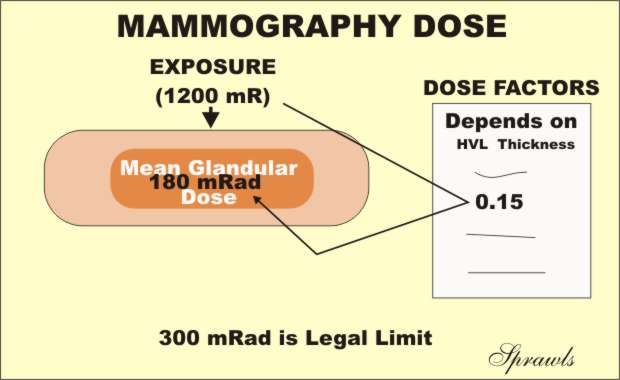
1. The first step is to determine the entrance surface exposure, or air kerma,
to the breast. This can be measured directly with small dosimeters placed
on the breast or calculated from the know calibration factors for the
mammography equipment.
2. Then, the MGD is determined by multiplying the surface exposure value by
published dose factors. The dose factor values are tabulated according to
breast size and composition and the penetrating characteristics of the x-ray
beam as determined by the anode material, filtration, and KV.
For comparison of imaging techniques, evaluation of equipment performance, general dose management, and regulatory and accreditation purposes, the MGD to a "standard" breast is used. The standard is a 4.2cm thick compressed breast consisting of 50% glandular tissue and 50% fat. This corresponds to the standard phantom that is used for image quality evaluation and comparative dose determinations.
Integral Dose
As we have just observed, absorbed dose, including the special
dose quantities; CTDI and MGD, all describe the concentration of radiation
energy absorbed in tissue. The units were the gray (1 joule/kg) or the rad
(100 ergs/gm) of tissue. While knowing the dose to a specific tissue
location or organ is often valuable information, it does not tell the full story
about how much total radiation energy is deposited in a body. Integral
dose is the radiation quantity that is equal to the total energy absorbed by the
body.
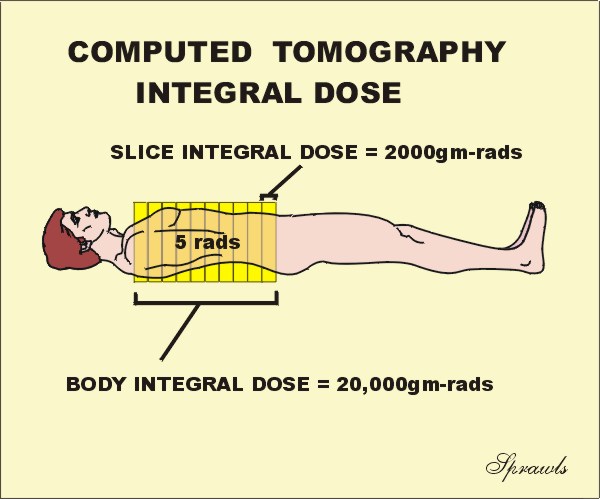 The
SI unit for integral dose is the joule (the standard unit of energy), and the
conventional unit is the gram-rad. Let's now use this CT illustration to
distinguish between the two quantities, dose and integral dose, and do it with a
question. Let's assume that first the patient was scanned for just one
slice, and the dose to the slice was 5 rads. Now, the scanning was
continued to include a total of 10 slices. Now the question...what was the
dose to the patient for the 10-slice scan? Are you going to say 50 rads?
Let's think about it. Remember dose is a concentration of absorbed
radiation energy. When the additional 9 slices were scanned, covering
different tissue, it did not change the concentration (dose) to the tissues, it
just exposed more tissue with the same dose, 5 rads. Therefore, when the number
of slices was increased, the integral dose, or total energy absorbed in the
body, was increased, but the absorbed dose (concentration) was not.
The
SI unit for integral dose is the joule (the standard unit of energy), and the
conventional unit is the gram-rad. Let's now use this CT illustration to
distinguish between the two quantities, dose and integral dose, and do it with a
question. Let's assume that first the patient was scanned for just one
slice, and the dose to the slice was 5 rads. Now, the scanning was
continued to include a total of 10 slices. Now the question...what was the
dose to the patient for the 10-slice scan? Are you going to say 50 rads?
Let's think about it. Remember dose is a concentration of absorbed
radiation energy. When the additional 9 slices were scanned, covering
different tissue, it did not change the concentration (dose) to the tissues, it
just exposed more tissue with the same dose, 5 rads. Therefore, when the number
of slices was increased, the integral dose, or total energy absorbed in the
body, was increased, but the absorbed dose (concentration) was not.
It is generally assumed that the risk of cancer induction is related to the
integral dose because it takes into account the amount of tissue exposed.
Computed
Tomography Dose Length Product
We recall that the CTDI is the practical quantity for
specifying dose in CT procedures. The associated quantity for
specifying the "total radiation" to a patient is the dose length product (DLP)
as illustrated here.
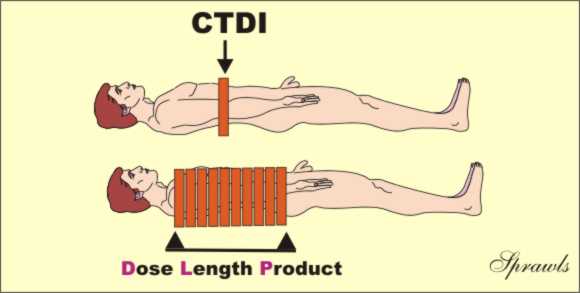 The
DLP is just the product of the CTDI value and the length of the body area
scanned. It has the units of either rad-cm or Gy-cm. It is a useful
and practical quantity for comparing the total radiation to patients for
various CT procedures. It is however, not a precise measure of the total
radiation or integral dose, that is more difficult to determine.
The
DLP is just the product of the CTDI value and the length of the body area
scanned. It has the units of either rad-cm or Gy-cm. It is a useful
and practical quantity for comparing the total radiation to patients for
various CT procedures. It is however, not a precise measure of the total
radiation or integral dose, that is more difficult to determine.
Dose Equivalent
All of the quantities that we have discussed up to this point
have been physical quantities. That is they are quantities that can
be measured and expressed in terms of the more fundamental physical quantities
like energy. However, a major reason for determining the amount of
radiation delivered to a body is to relate it to biological effects or the
biological impact of the radiation on the body. This brings another factor
into consideration. That is various types of radiation might not produce
the same biological impact, even when the dose or energy delivered to the tissue
is the same. In other words, just knowing the (physical) dose does not
tell the whole story.
Dose Equivalent, in the unit, sievert (Sv), is a quantity that expresses the relative biological impact of the radiation by including a radiation weighting factor (wR). The relationship is:
|
Dose Equivalent (Sv) = Dose (Gy) x wR |
The value of the radiation weighting factor (wR) is a characteristic of each specific type of radiation. What makes it easy is that the radiations we use for medical imaging (x-ray, gamma, beta, positron) all have radiation weighting factor (wR) values of one (1). Therefore, for our types of radiations:
|
Dose Equivalent (Sv) = Dose (Gy) |
Some other types of radiation, like the larger particles, might have higher values for wR. What this means is that these radiations will produce more biological effect per unit of absorbed dose.
Where we will most often encounter dose equivalent is in expressing the radiation received by personnel working in radiation environments, etc. For example, the values measured with personnel monitoring devices (film badges, TLDs, etc) are usually reported in sieverts.
Effective Dose
Effective dose is becoming a very useful radiation quantity for
expressing relative risk to humans, both patients and other personnel. It
is actually a simple and very logical concept. It takes into account the
specific organs and areas of the body that are exposed. The point is that
all parts of the body and organs are not equally sensitive to the possible
adverse effects of radiation, such as cancer induction and mutations.
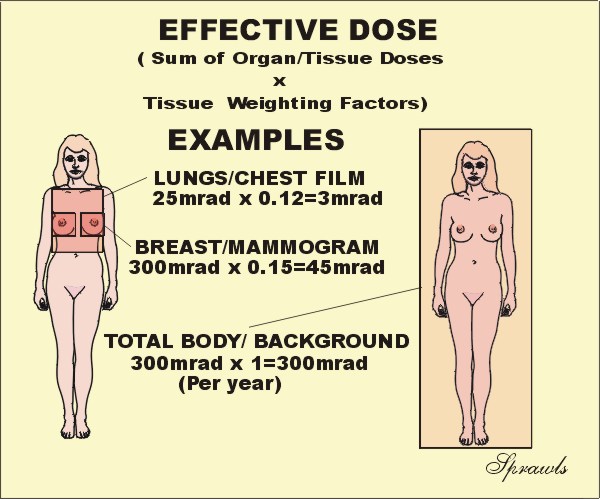 For
the purpose of determining effective dose, the different areas and organs have
been assigned tissue weighting factor (wT)
values. For a specific organ or body area the effective dose is:
For
the purpose of determining effective dose, the different areas and organs have
been assigned tissue weighting factor (wT)
values. For a specific organ or body area the effective dose is:
|
Effective Dose (Gy) = Absorbed Dose (Gy) x wT |
If more than one area has been exposed, then the total body effective dose is just the sum of the effective doses for each exposed area. It is a simple as that. Now let's see why effective dose is such a useful quantity. There is often a need to compare the amount of radiation received by patients for different types of x-ray procedures, for example, a chest radiograph and a CT scan. The effective dose is the most appropriate quantity for doing this. Also, by using effective dose it is possible to put the radiation received from diagnostic procedures into perspective with other exposures, especially natural background radiation.
It is generally assumed that the exposure to natural background radiation is somewhat uniformly distributed over the body. Since the tissue weighting factor for the total body has the value of one (1), the effective dose is equal to the absorbed dose. This is assumed to be 300 mrad in the illustration.
Let's look at an illustration. If the the
dose to the breast ,MGD, is 300 mrad for two views, the effective dose is 45
mrad because the tissue weighting factor for the breast is 0.15.
What this means is that the radiation received from one mammography procedure is
less than the typical background exposure for a period of two months.
Tissue Weighting Factors
| Tissue | Weighting Factor |
| Gonads |
0.25 |
| Breast | 0.15 |
| Red Bone Marrow |
0.12 |
| Lung | 0.12 |
| Thyroid | 0.03 |
| Bone Surface | 0.03 |
| Remainder | 0.3 (For the remaining organs a value of 0.06 is used for each of the five organs receiving the highest dose.) |
| Total Body | 1.0 |