INTRODUCTION AND OVERVIEW

Statistical Photon Fluctuation As a Source of Counting Error and Image Noise
 

   The random emission of photons with respect to location, or area, produces image noise. The presence of this spatial noise within an image decreases the ability to see and detect low-contrast objects.

   In this chapter we first consider the nature of the random variation, or fluctuation, in photons from a radioactive source, and then show how this knowledge can be used to increase the precision of activity measurements (counting) and the quality of nuclear images.  The same general statistics applies to photons in an x-ray beam.

   We must first know something about the extent of the fluctuation that is the source of error and image noise, and if it is related to a factor over which we have control. One approach is to imagine we are conducting an experiment for the purpose of studying the random nature of photon emissions. Let us assume we have a source of radiation in a scintillation well counter that is being counted again and again for 1-minute intervals. We quickly notice that the number of counts, or photons, varies from one interval to another. Some of the values we observe might be 87, 102, 118, 96, 124, 92, 108, 73, 115, 97, 105, and 82. Although these data show that there is a fluctuation, they do not readily show the range of fluctuations. The amount of fluctuation will become more apparent if we arrange our data in the form of a graph, as shown in the figure below. In this graph, we plotted the number of times we measured a specific number of counts versus the actual number of counts observed. Obviously, we would have to count the number of photons from our source many many times to obtain the data to plot this type of graph.

Graph Showing the Relative Number of Times Different Count Values (Number of Counts) Are Obtained
When a Specific Radioactive Sample Is Counted Again and Again

   When the data are presented in this manner, it is apparent that some count values occurred more frequently than others. In our experiment we observed 100 counts more frequently than any other value. Also, most of the count values fell within the range of 70 to 130 counts. Within this range, the number of times we observed specific count values is distributed in the Gaussian, or normal, distribution pattern. (This is actually a special type of Gaussian distribution known as the Poisson distribution and is discussed later.)

   At this point we need to raise a very significant question:  Of all of these values, which one is the "true" count rate that best represents the activity of our sample? In our example, the average, or mean, of all of the values is 100 counts. This is considered to be the value that best represents the true activity of the sample.

COUNTING ERROR

The Amount of Error Is the Difference between the Measured and True Count Values

   Error Ranges

CONTENTS

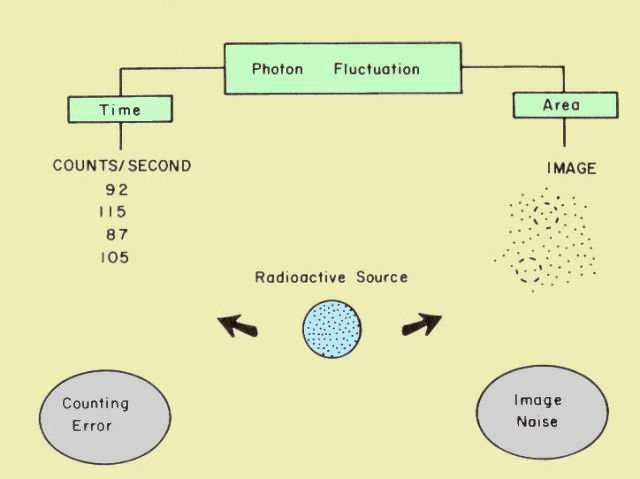
   From our earlier experiment, we know that the value of any individual count falls within a certain range around the true count value. In our experiment, we observed that all counts fell within 30 counts (plus or minus) of the true value (100 counts). Based on this observation, we could predict the maximum error that could occur when we make a single count. In our case. the maximum error would be ± 30 counts ( ± 30%). We also observed that very few count values approached the maximum error. In fact, a large proportion of the count values are clustered relatively close to the true value. In other words, the error associated with many individual counts is obviously much less than the maximum error. To assume that the error in a single count is always the maximum possible error is overstating the problem. Although it is necessary to recognize that a certain maximum error is possible, we must be more realistic in assigning values to the error itself because it is usually much less than the maximum possible error.

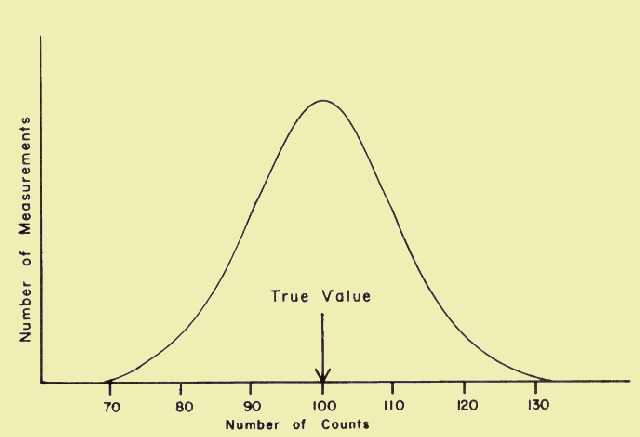
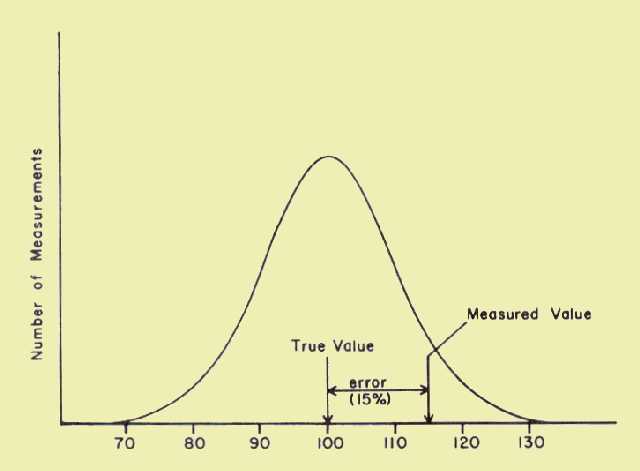
   If, at this point, we were to go back to the data from our earlier experiment and analyze it from the standpoint of how the individual count values are clustered around the true value (mean), we would get results similar to those illustrated in the following figure. For the purpose of this analysis, we established three error ranges around the true value. In our particular case, the error ranges are in ten-count increments. The first range is ± 10 counts (10% error), the second range is ± 20 counts (20% error), and the largest range is ± 30 counts (30% error). At this point we are interested in how often the value of a single measurement fell within the various error ranges. Upon careful analysis of our data, we find that 68% of the time the count values are within the first error range ( ± 10%), 95% of all count values are within the next error range (± 20%), and essentially all values (theoretically 99.7%) are within the largest error range ( ± 30%).

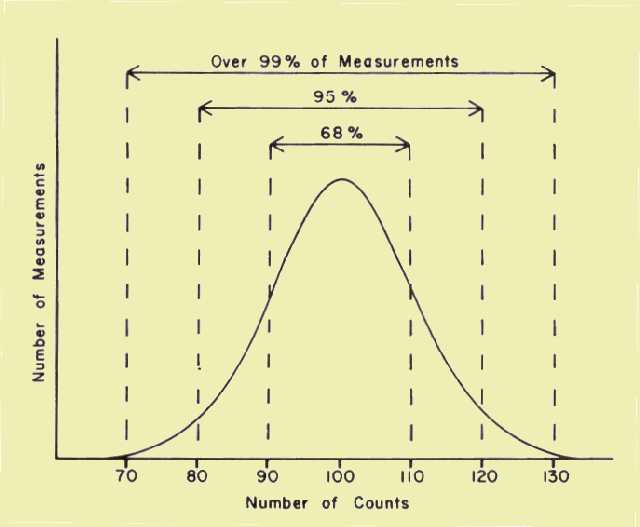
Number of Measurements That Fall within Specific Error Ranges

   With this information as background, let us now see what we can say about the error of an individual measurement. Note that in the case of a single measurement, there is no way to determine the actual error because the true value is unknown. Therefore, we must think in terms of the probability of being within certain error ranges. With this in mind, we can now make several statements concerning the error of an individual measurement in our earlier experiment:

• There is a 68% probability (chance) that the error is within ± 10%.

• There is a 95% probability that the error is within ± 20%.

• There is a 99.7% probability that the error is within ± 30%.

   While we are still not able to predict what the actual error is, we can make a statement as to the probability that the error is within certain stated limits.
 

   It might appear that the error ranges used above were chosen because they were in simple increments of ten counts. Actually, they were chosen because they represent "standard" error ranges used for values distributed in a Gaussian manner. Error ranges can be expressed in units, or increments, of standard deviations (s). In our example, one standard deviation (s) is equivalent to ten counts. However, one standard deviation is not always equivalent to ten counts.

   The general situation is illustrated in the figure which follows the table below. For values distributed in a Gaussian manner, the relationship between the probability of a value falling within a specific error range remains constant when the error range is expressed in terms of standard deviations. For the general case, we have the following relationship between error limits and the probability of a value falling within the specific limits:

Error Limits                     Probability

± 1s                             68.0%
± 2s                             95.0%
± 3s                             99.7%

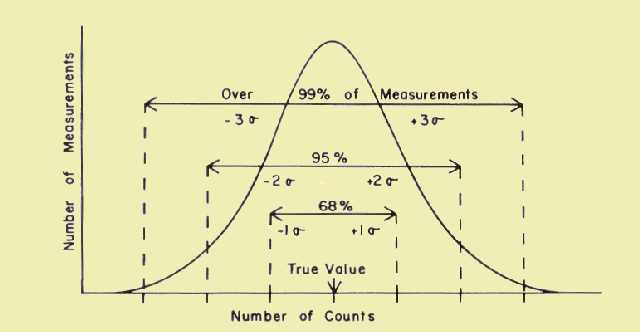
Relationship between the Number of Measurements within Error Limits When the Limits
Are Expressed in Terms of Standard Deviations

   It might be helpful to draw an analogy between the error limits and a bull's-eye target, as shown below. The small bull's-eye in the center represents the true count value for a specific sample. If we make one measurement, we can expect the count value to "hit" somewhere within the overall target area. Although there is no way to predict where the value of a single measurement will fall, we do know something about the probability, or chance, of it falling within certain areas. For example, there is a 68% chance that our count value will fall within the smallest circle, which represents an error range of one standard deviation. There is a 95% probability that the value will fall within the next largest circle, which represents an error range of two standard deviations. Essentially all of the values (99.7%) will fall within the largest circle, which represents an error range of three standard deviations.

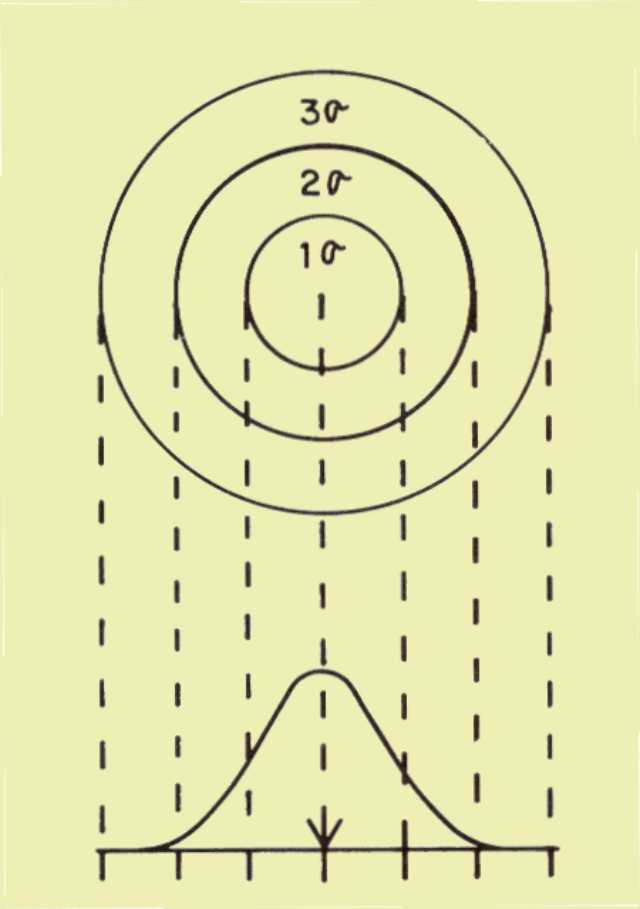
An Analogy between Counting Error and a Bull's-Eye Target

   Measuring the relative activity of a radioactive sample is like shooting at a bull's-eye. We do not expect to get the true count value (hit the bull's-eye) each time. The problem is that after making a measurement (taking a shot) we do not know what our actual error is (by how far we missed the bull's-eye). This is because we do not know what the true value is, only the value of our single measurement. We must, therefore, describe our performance in terms of error ranges and the confidence we have of falling within the various ranges. We can express a level of confidence of falling within a certain error range if we know the probability of a single value falling within that range. For Gaussian distributed count values, 68% will fall within one standard deviation of the true, or mean, value. Based on this we could make the statement that we are 68% confident that the value of a single measurement will fall within the one standard deviation error range. A more complete description of our performance could be summarized as follows:

Error Range             Confidence Level

± 1s                           68.0%
± 2s                           95.0%
± 3s                           99.7%

   A clear distinction between an error range and a confidence level is necessary. Error range describes how far a single measurement value might deviate, or miss, the true count value of a sample. Confidence level expresses the probability, or chance, that a single measurement will fall within a specific error range. Notice that as we increase the size of our error range our confidence level also increases. In terms of our target, this simply means we are more confident that our shot will hit within a larger circle than within a smaller circle.

   The relationship between confidence level and error range expressed in standard deviations does not change for measurement values distributed in a Gaussian manner. What does change, however, is the relationship between an error range expressed in standard deviations and an error range expressed in actual number of counts or percentages. In our earlier example, one standard deviation was equal to ten counts, or 10%. We will now find that for other measurements one standard deviation can be a different number of counts.

   Radiation events (such as count values), unlike the value of many other non-radiation variables, are distributed in a very special way. The value of the standard deviation, expressed in number of counts, is related to the actual number of photons counted during the measurement. Theoretically, the value of the standard deviation is the square root of the mean of a large number of measurements. In actual practice, we never know what the true count value of a sample is. In most cases, our measurement value will be sufficiently close to the true value so that we can use it to estimate the value of the standard deviation as follows:

                                      ______________
Standard deviation = √Measured value.

   For example, if we make a measurement in which 100 counts will be recorded, the value of the standard deviation will be

___
         s    =  √100  =  10 counts.

   This will be recognized as the count value in our earlier example, where it was stated that the value of one standard deviation was 10 counts, or 10%. Now let us examine the values of one standard deviation for other recorded count values shown in Table 1. Examination of this table shows that as the number of counts recorded during a single measurement increases, the value of the standard deviation, in number of counts, also increases; but it decreases when expressed as a percentage of the total number of counts. We can use this last fact to improve the precision of radiation measurements.

   The error range, expressed as a percentage of the measured value, decreases as the number of counts in an individual measurement is increased. The real significance of this is that the precision of a radiation measurement is determined by the actual number of counts recorded during the measurement. The error limits for different count values and levels of confidence are shown in Table 2.
 

   We can use the information in Table 2 to plan a radiation measurement that has a specific precision. For example, if we want our measurement to be within a 2% error range at the 95% confidence level, it will be necessary to record at least 10,000 counts. Most radiation counters can be set to record counts either for a specific time interval or until a specific number of counts are accumulated. In either case, the count rate of the sample (relative activity) is determined by dividing the number of counts recorded by the amount of time. Presetting the number of counts and then measuring the time required for that number of counts to accumulate allows the user to obtain a specific precision in the measurement.

Combined Errors when Subtracting and Adding

CONTENTS

   In some applications, it is necessary to add or subtract counts in order to obtain a desired parameter. One example is the subtraction of background from a sample measurement. Another example is the subtraction of one x-ray image from another as in digital-subtraction angiography.

Here we will consider the process of measuring radioactivity. The first step is to count the sample. (Counts from background radiation are included in this measurement.) The next step is to remove the radioactive sample from the counting system, and then measure only the background radiation. The background count rate is then subtracted from the sample-plus-background count rate to obtain a measurement of the relative sample activity. The question now arises: What is the error in the sample count rate that was obtained by subtracting one count value from another?

   Let us use the example shown below to investigate the error in the difference between two count values. Assume that we have two radiation sources. For the same counting time, one has a true value of 3,600 counts and the other a true value of 6,400 counts. The true difference between the two is 2,800 counts. If we now measure the two samples, we expect the measured values to fall somewhere within the error ranges indicated in the figure below. With respect to the measured difference we now have two errors to contend with, one for each of the sample measurements. The question is now: What will be the error range for the difference between the two measured values? In some instances, the error in the measurement of one sample might be in a direction that compensates for the error in the measurement of the other sample, and the net error in the difference would be relatively small. There is also the possibility that the two errors are in opposite directions, in which case the error in the difference would be relatively large.

Errors Associated with the Difference between Two Count Values

   When making measurements on two samples, we have no way of knowing either the amount or direction of the individual errors. Therefore, we must consider the range of errors possible in the difference between the two measured count values. Because of the possibility of errors compounding (by being in opposite directions), it should be obvious that the error range for the difference (s_d) will be larger than the error range associated with the individual measurement (s₁ and s₂). When the error ranges are expressed in terms of standard deviations, the relationship becomes

          ________
s_d = √s₁² + s₂².

   Let us now examine the actual values in the figure above and see what the error range will be for the difference between the two count values. The first sample measurement has a true value of 3,600 counts. By taking the square root of this number, we find that the standard deviation is 60 counts, or 1.67%. The second sample has a count total of 6,400 counts with a standard deviation of 80 counts, or 1.25%. If we now determine the standard deviation for the difference by using the relationship given above, we see that

   A standard deviation of 100 counts is 3.6% of the difference between the two count values, 2,800 counts.

   Any time we add or subtract count values, the error range (standard deviation) of the sum or difference will be larger than the error range of the individual measurements. When two count values are added, the standard deviation of the sum (s_s) is related to the standard deviation of the individual measurements (s₁ and s₂) by

   Notice that this is the same relationship as that for the difference between two count values. A common mistake is to assume that the sign between the two standard deviation values is different for addition and subtraction. It does not change; it is positive in both cases.

   Let us now determine the error range of the sum of the two count values in the above figure. As we have just seen, the standard deviation for the sum is the same as the standard deviation for the difference. That is, in this case, 100 counts, but since the sum of the two count values is 10,000 counts this now represents an error range of only 1 %. This is the same error range as we would find on a single measurement of 10,000 counts.

   When expressed as a percentage, the error range increases when we take the difference between two measurements, but it decreases when we add the results of the two measurements.

When applied to imaging:

• Subtracting one image from another increases the noise.
   

• Adding or averaging images together decreases the noise.

This is discussed in much more detail in the section on Image Noise.