QUANTITIES

CONTENTS

   Radiation quantities used to describe a beam of x-radiation fall into two general categories as shown here. One category comprises the quantities that express the total amount of radiation, and the other comprises the quantities that express radiation concentration at a specific point. We need to develop this distinction before considering specific quantities.

Radiation Quantities and Units

   A characteristic of an x-ray beam or any other type of radiation emitted from a relatively small source is that it is constantly spreading out or diverging as it moves away from the source, as shown below. At any point along the beam, the width of the area covered is proportional to the distance from the source. At a distance of 1 m, the cross-sectional beam area is one unit wide and progresses to a width of two units at a distance of 2 m. At 3 m, the area is three units wide. Therefore, the area covered by our x-ray beam is increasing in proportion to the square of the distance from the source.

Inverse-Square Effect

   First, let us consider the amount of radiation passing through the three areas. We are assuming that none of the radiation is absorbed or removed from the beam before it reaches the third area. All radiation that passes through the first area will also pass through the second and third areas. In other words, the total amount of radiation is the same through all areas and does not change with distance from the source.

   Now let us consider the concentration of radiation through the three areas. In the first area, all radiation is concentrated in a one-unit area. At a distance of 2 m from the source the radiation is spread over a four-unit square area, and continues to spread to cover a nine-unit square area at a distance of 3 m. If the same total amount of radiation is being distributed over larger areas it is obviously becoming less concentrated.

   What we have observed here is the fact that as radiation moves away from its source, the total amount of radiation does not change but its concentration decreases. At any given distance the concentration is inversely proportional to the area covered by the beam, and the area covered by the beam is proportional to the square of the distance from the source. We can conclude that the concentration of radiation is inversely related to the square of the distance from the source. This is commonly known as the inverse-square law.

   We now introduce some quantities and the associated units that can be used to express both the concentration and total amount of radiation.

PHOTONS

CONTENTS

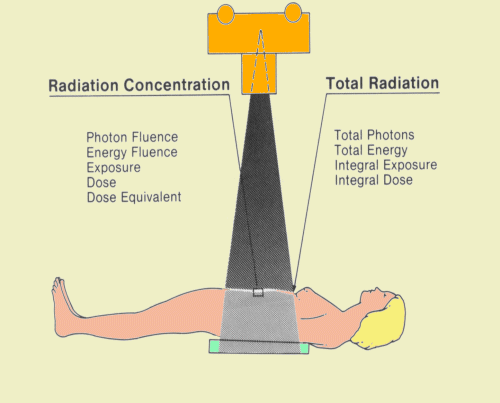
     Since an x-ray beam and gamma radiation are showers of individual photons, the number of photons could, in principle, be used to express the amount of radiation. In practice, the number of photons is not commonly used, but it is a useful concept in understanding the nature of radiation and distinguishing between concentration and total radiation. Let us go back to the situation shown above and examine the different ways the concentration of radiation delivered to a small area on a patient's body could be expressed.

Photon Concentration (Fluence)

CONTENTS

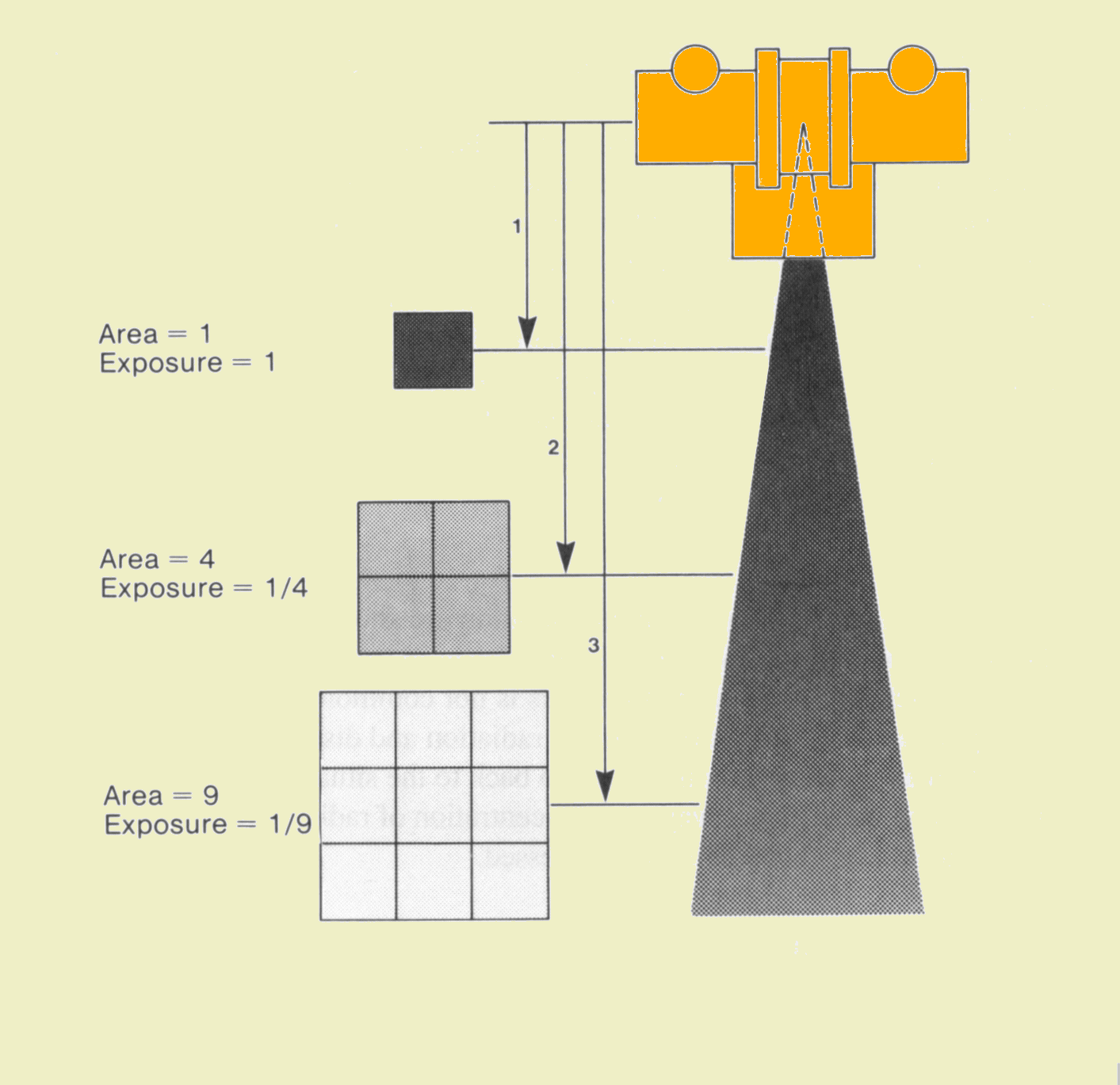
   If we draw a 1- cm² area on the surface of the patient and then count the number of photons passing through the area during a radiographic procedure, we will have an indication of the concentration of radiation delivered to the patient. During a single abdominal radiographic exposure we would find that close to 1010 photons would have passed through our square centimeter. The more formal term for photon concentration is photon fluence. 

 Total Photons

CONTENTS

   If we count the number of photons entering the total exposed area, we will have an indication of the total amount of radiation energy delivered to the patient. This quantity depends on the size of the exposed area and the radiation concentration. If the radiation is uniformly distributed over the exposed area, the total number of photons entering the patient can be found by multiplying the concentration (fluence) by the exposed area. Changing the size of the exposed area does not affect the concentration entering at the center of the beam. However, reducing the exposed area does reduce the total number of photons and radiation entering the patient.

EXPOSURE

CONTENTS

    Concept

   Exposure is the quantity most commonly used to express the amount of radiation delivered to a point. The conventional unit for exposure is the roentgen (R), and the Sl unit is the coulomb per kilogram of air (C/kg):

1 R = 2.58 x 10^-4 C/kg

1 C/kg = 3876 R

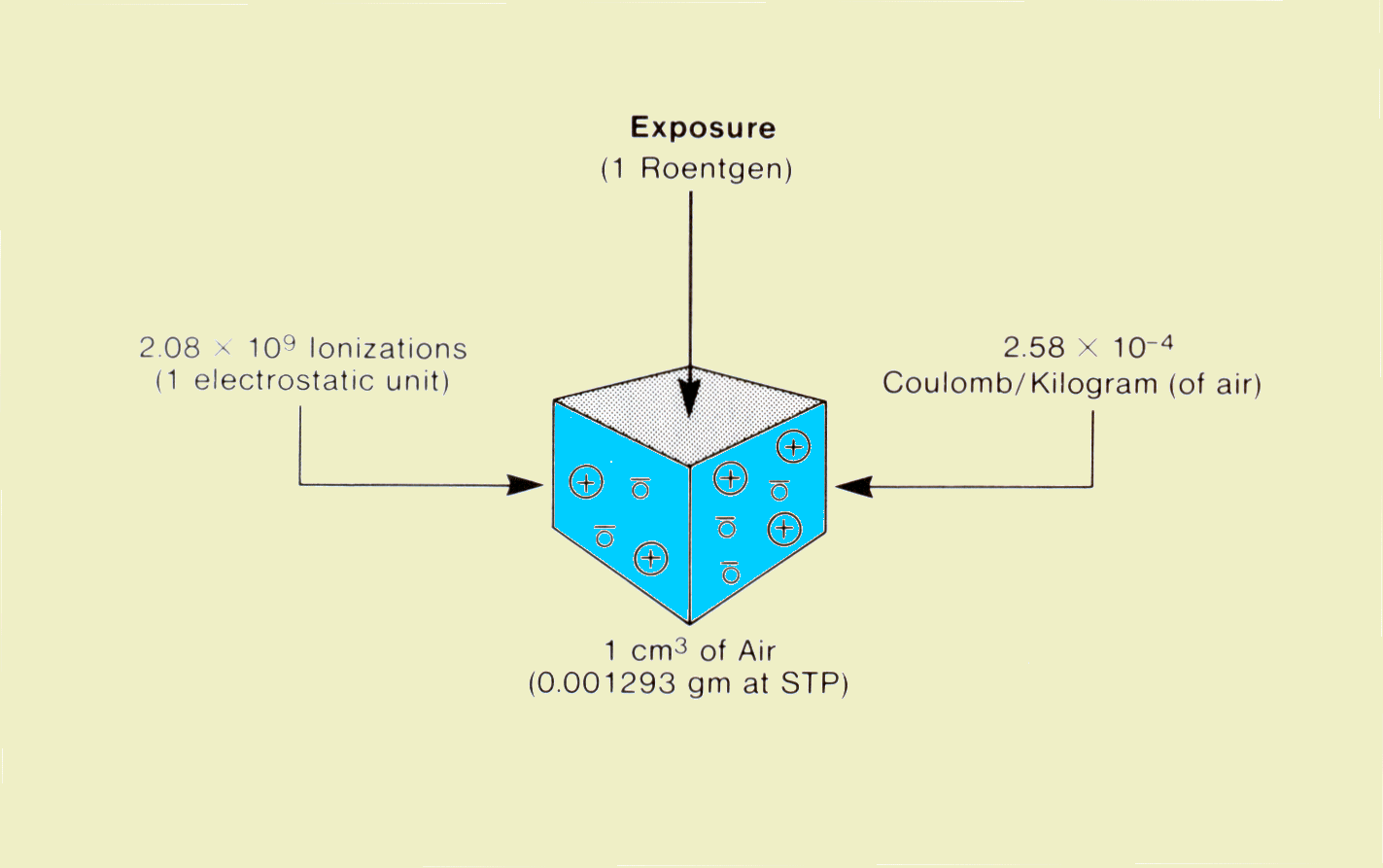
The reason exposure is such a widely used radiation quantity is that it can be readily measured. All forms of radiation measurement are based on an effect produced when the radiation interacts with a material. The specific effect used to measure exposure is the ionization in air produced by the radiation.

Exposure

  Exposure is generally measured by placing a small volume of air at the point of measurement and then measuring the amount of ionization produced within the air. The enclosure for the air volume is known as an ionization chamber. The use of ionization chambers and other radiation measuring devices is discussed in Chapter 42. The concept of exposure and its units can be developed from the figure above. When a small volume of air is exposed to ionizing radiation (x-ray, gamma, etc.), some of the photons will interact with the atomic shell electrons. The interaction separates the electrons from the atom, producing an ion pair. When the negatively charged electron is removed, the atom becomes a positive ion. Within a specific mass of air the quantity of ionizations produced is determined by two factors: the concentration of radiation photons and the energy of the individual photons.

   An exposure of 1 roentgen produces 2.08 x 10⁹ ion pairs per cm³ of air at standard temperature and pressure (STP); 1 cm³ of air at STP has a mass of 0.001293 g. The official definition of the roentgen is the amount of exposure that will produce 2.58 x 10^-4 C (of ionization) per kg of air. A coulomb is a unit of electrical charge. Since ionization produces charged particles (ions), the amount of ionization produced can be expressed in coulombs. One coulomb of charge is produced by 6.24 x 10¹⁸ ionizations.

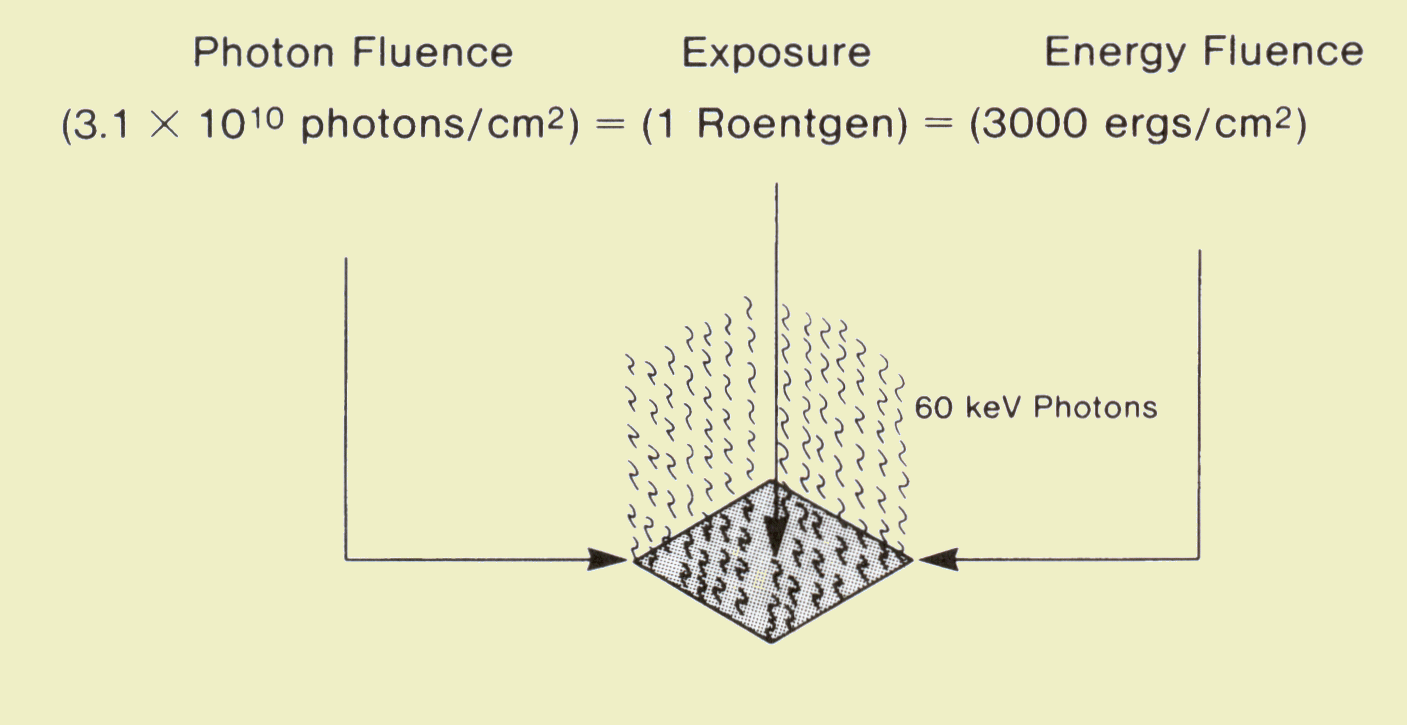
Exposure is a quantity of radiation concentration. For a specific photon energy, exposure is proportional to photon concentration or fluence. The relationship between exposure and photon concentration is shown below; the relationship changes with photon energy because both the number of photons that will interact and the number of ionizations produced by each interacting photon is dependent on photon energy. If we assume a photon energy of 60 keV, a 1-R exposure is equivalent to a concentration of approximately 3 x 10¹⁰ photons per cm².

Relationship between Exposure and Photon Concentration

 AIR KERMA

CONTENTS

 Air kerma is another radiation quantity that is sometimes used to express the radiation concentration delivered to a point, such as the entrance surface of a patient's body.  It is a quantity that fits into the SI scheme.

 Surface Integral Exposure

CONTENTS

Since exposure expressed in roentgens or coulombs per kilogram is a concentration, it does not express the total amount of radiation delivered to a body. The total radiation delivered, or surface integral exposure (SIE), is determined by the exposure and the dimensions of the exposed area. It is also referred to as the exposure-area product.

The surface integral exposure is expressed in the conventional units of roentgens-square centimeters (R-cm²). If the radiation exposure is uniform over the entire area, the SIE is the product of the exposure in roentgens and the exposure area in square centimeters. If the exposure is not the same at all points in the exposed area, the SIE can be found by adding the exposure values for each square centimeter of exposed surface. Mathematically, this is the process of integrating the exposure over the surface area. The SIE can be measured during x-ray examinations by placing a special type of ionization chamber in the x-ray beam. The significance of SIE is that it describes total radiation imparted to a patient, whereas exposure indicates only the concentration of radiation at a specified point.

The typical fluoroscopy examination provides an excellent opportunity to compare exposure (concentration) and SIE (total radiation). In the figure below two cases are compared. In both instances the beam area was 10 cm x 10 cm (100 cm²); the total exposure time was 5 minutes at an exposure rate of 3 R/min. In both instances the SIE is 1,500 R- cm². However, the exposure depends on how the x-ray beam was moved during the examination. In the first example the beam was not moved and the resulting exposure was 15 R. In the second example, the beam was moved to different locations so that the exposure was distributed over more surface area and the concentration became less.

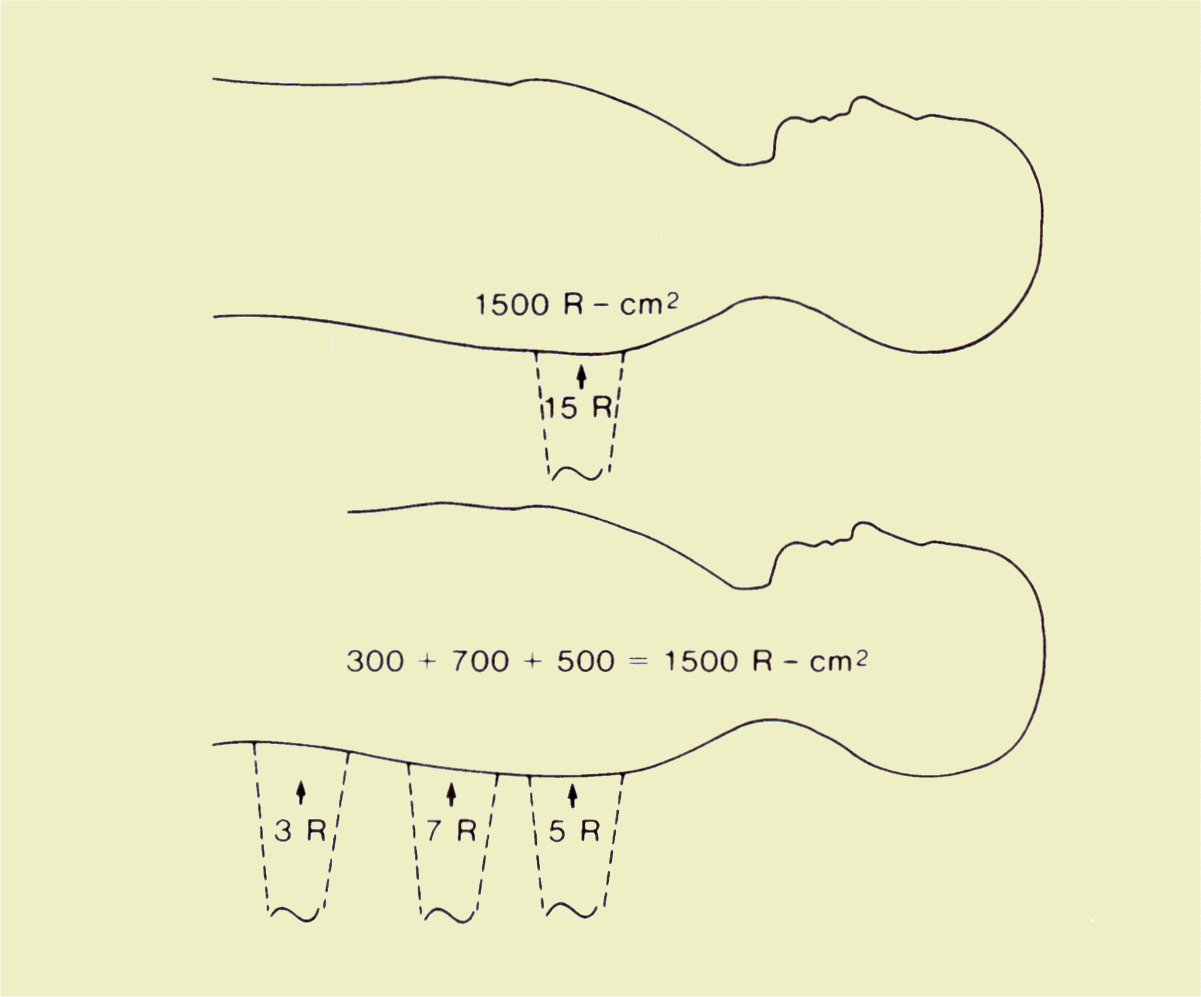Comparison of SIE and Exposure during a Fluoroscopic Examination

Another important example is illustrated below. Here the same exposure (100 mR) is delivered to both patients. However, there is a difference in the exposed area: the patient on the right received 10 times as much radiation as the patient on the left.

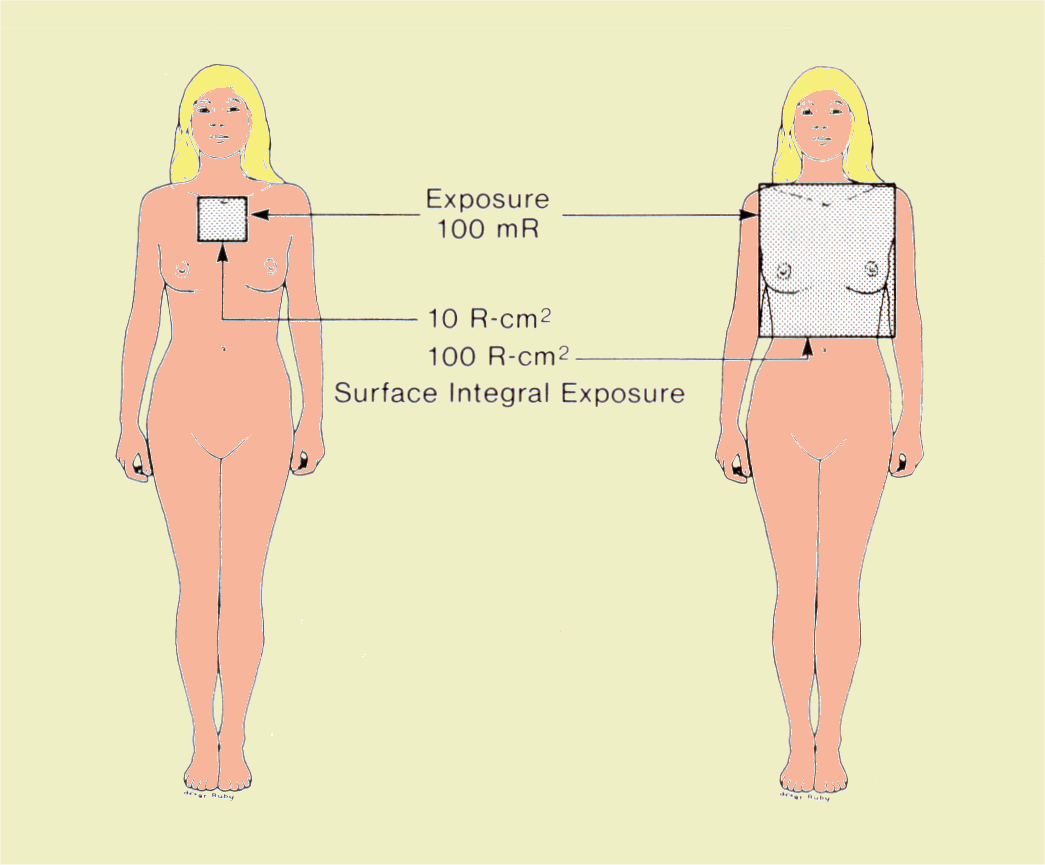Comparison of SIE Values for a Radiographic Examination

Dose Area Product (DAP)

CONTENTS

The important point to remember is that exposure (roentgens) alone does not express the total radiation delivered to a body. The total exposed area must also be considered.

ENERGY

CONTENTS

An x-ray beam and other forms of radiation deliver energy to the body. In principle, the amount of radiation delivered could be expressed in units of energy (joules, ergs, kiloelectron volts, etc.). The energy content of an x-ray beam is rather difficult to measure and for that reason is not widely used in the clinical setting. However, considering the energy delivered by an x-ray beam is helpful in understanding other radiation quantities.

 Energy Fluence

CONTENTS

Energy fluence (concentration) is the amount of radiation energy delivered to a unit area. The units for expressing radiation energy concentration are either the millijoule (mJ) per square centimeter or erg per square centimeter. For a specific photon energy, fluence is proportional to exposure. The relationship between energy fluence and exposure is shown above, under "EXPOSURE". The relationship changes with photon energy because of the change in photon interaction rates. However, if we assume a photon energy of 60 keV, the energy fluence for a 1-R exposure is approximately 0.3 mJ/ cm².

The energy delivered by an x-ray beam can be put into perspective by comparing it to the energy delivered by sunlight, as shown below. For the x-ray exposure we will use the fluoroscopic factors of 5 minutes at the rate of 3 R/min. This 15-R exposure delivers x-ray energy to the patient with a concentration (fluence) of 4.5 mJ/cm² if we assume an effective photon energy of 60 keV.

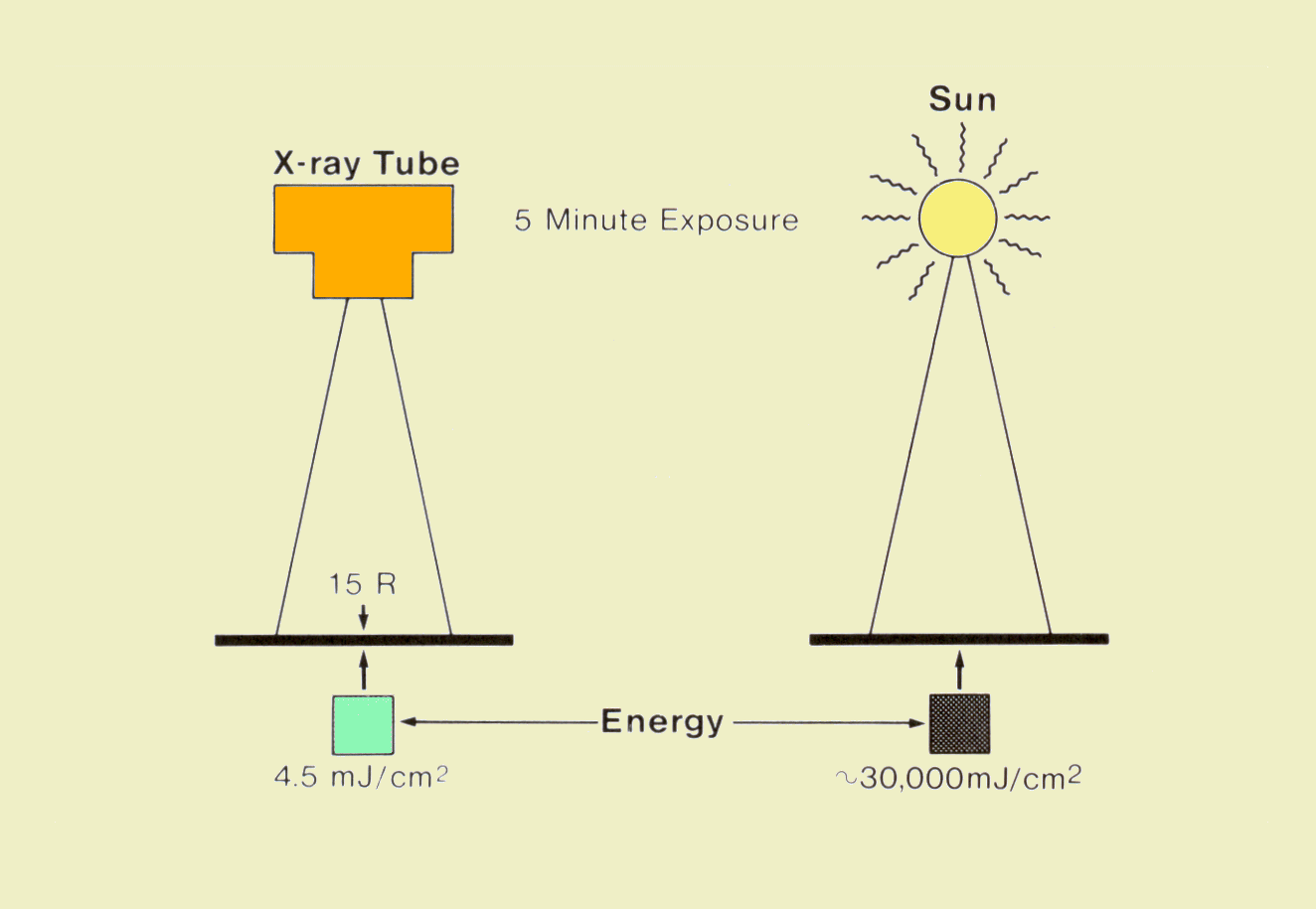Comparison of Energy Delivered by an X-Ray Beam and Sunlight

The energy delivered by the sun depends on many factors including geographic location, season, time of day, and atmospheric conditions; a typical midday summer exposure on a clear day in Atlanta produces approximately 100 mJ/sec/cm². In 5 minutes a person would be exposed to an energy fluence of 30,000 MJ/cm². We see from this example that the energy content of an x-ray beam is relatively small in comparison to sunlight. However, x-ray and gamma radiation will generally produce a greater biological effect per unit of energy than sunlight because of two significant differences: x- and gamma radiation penetrate and deposit energy within the internal tissue, and the high energy content of the individual photons produces a greater concentration of energy at the points where they are absorbed within individual atoms.

    Total Energy

The total energy imparted to a body by an x-ray beam is determined by the energy fluence (concentration) and the size of the exposed area. If the radiation is uniformly distributed over the area, the total energy delivered is the product of the fluence and the surface area.

ABSORBED DOSE

CONTENTS

    Concept

A human body absorbs most of the radiation energy delivered to it. The portion of an x-ray beam that is absorbed depends on the penetrating ability of the radiation and the size and density of the body section exposed. In most clinical situations more than 90% is absorbed. In nuclear imaging procedures, a large percentage of the energy emitted by radionuclides is absorbed in the body. Two aspects of the absorbed radiation energy must be considered: the amount (concentration) absorbed at various locations throughout the body and the total amount absorbed.

Absorbed dose is the quantity that expresses the concentration of radiation energy absorbed at a specific point within the body tissue. Since an x-ray beam is attenuated by absorption as it passes through the body, all tissues within the beam will not absorb the same dose. The absorbed dose will be much greater for the tissues near the entrance surface than for those deeper within the body. Absorbed dose is defined as the quantity of radiation energy absorbed per unit mass of tissue.

    Units

   The conventional unit for absorbed dose is the rad, which is equivalent to 100 ergs of absorbed energy per g of tissue. The SI unit is the gray (Gy), which is equivalent to the absorption of 1 J of radiation energy per kg of tissue. The relationship between the two units is

1 rad = 100 erg/g = 0.01 J/kg = 0.01 Gy

1 Gy = 100 rad

  For a specific type of tissue and photon energy spectrum, the absorbed dose is proportional to the exposure delivered to the tissue. The ratio, f, between dose (rads) and exposure (roentgens) is shown below for soft tissue and bone over the photon energy range normally encountered in diagnostic procedures. The absorbed dose in soft tissue is slightly less than 1 rad/R of exposure throughout the photon energy range. The relationship for bone undergoes a considerable variation with photon energy. For a typical diagnostic x-ray spectrum, a bone exposure of 1 R will produce an absorbed dose of approximately 3 rad.

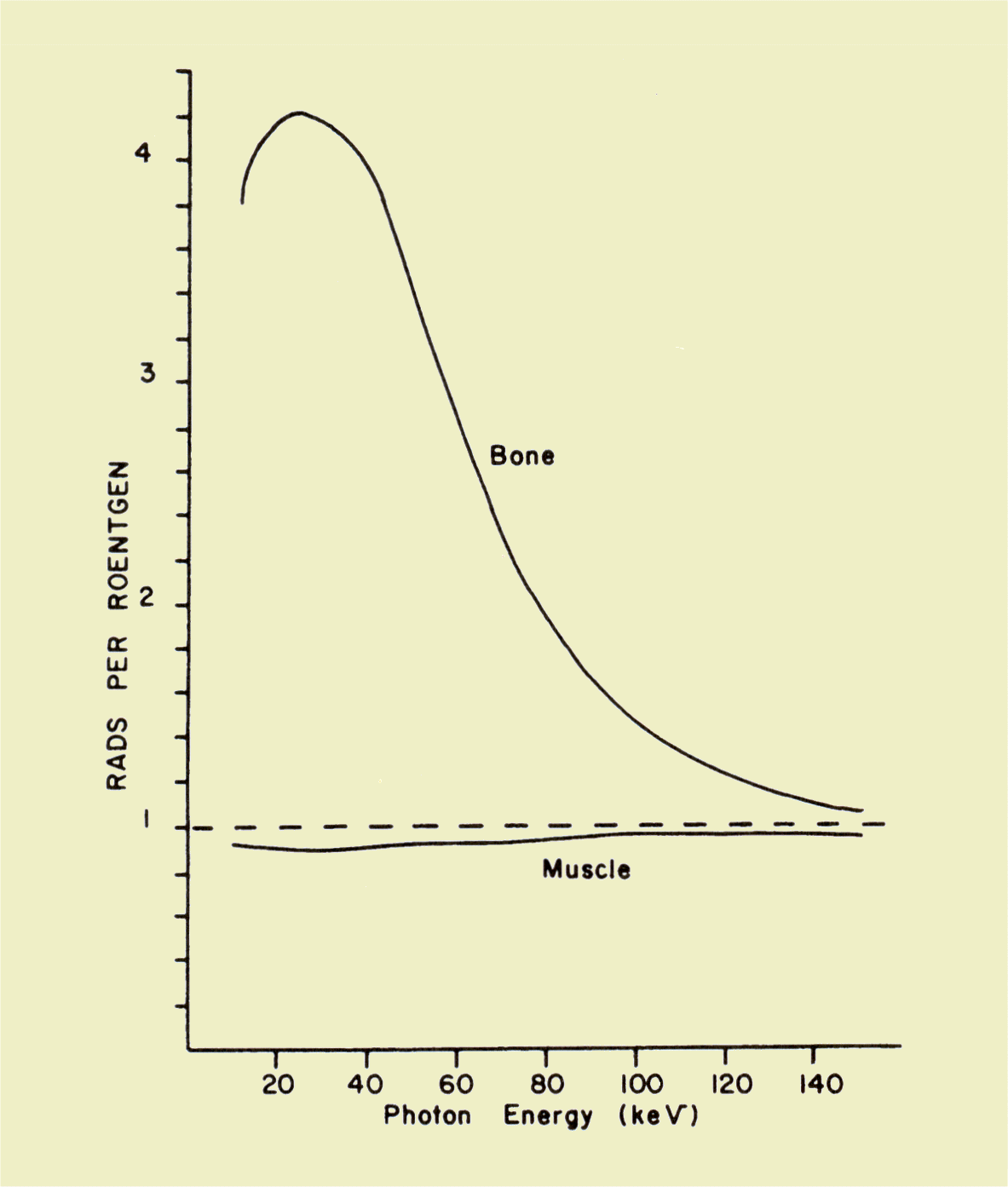Relationship of Absorbed Dose to Exposure

Computed Tomography Dose Index (CTDI)

CONTENTS

The Concept of Computed Tomography Dose Index (CTDI)
 

   The Computed Tomography Dose Index, CTDI, is the special dose quantity that is used extensively to express absorbed dose in CT.

Mean Glandular Dose (MGD)

CONTENTS

Mean Glandular Dose (MGD) in the Breast
 

   The Mean Glandular Dose (MGD) is the special dose quantity used in mammography.  It is defined as the mean, or average, dose to the glandular tissue within the breast.  The assumption is that the glandular tissue, and not the fat, is the tissue at risk from radiation exposure.  Obviously, it is just about impossible to determine the actual dose to the glandular tissue during a specific mammographic procedure because of variations in breast size and distribution of glandular tissue within the breast.  The MGD is based on some standard breast parameters.

    MGD values are determined by following a standard two-step protocol:

   1. The first step is to determine the entrance surface exposure, or air kerma, to the breast.  This can be measured directly with small dosimeters placed on the breast or calculated from the known calibration factors for the mammography equipment.

   2. Then, the MGD is determined by multiplying the surface exposure value by published dose factors.  The dose factor values are tabulated according to breast size and composition and the penetrating characteristics of the x-ray beam as determined by the anode material, filtration, and KV.

For comparison of imaging techniques, evaluation of equipment performance, general dose management, and regulatory and accreditation purposes, the MGD to a "standard" breast is used.  The standard is a 4.2cm thick compressed breast consisting of 50% glandular tissue and 50% fat.  This corresponds to the standard phantom that is used for image quality evaluation and comparative dose determinations.

 Integral Dose

CONTENTS

  Integral dose is the total amount of energy absorbed in the body. It is determined not only by the absorbed dose values but also by the total mass of tissue exposed.

  The conventional unit for integral dose is the gram-rad, which is equivalent to 100 ergs of absorbed energy. The concept behind the use of this unit is that if we add the absorbed doses (rads) for each gram of tissue in the body, we will have an indication of total absorbed energy. Since integral dose is a quantity of energy, the SI unit used is the joule. The relationship between the two units is

1 J = 1,000 gram-rad

  Integral dose (total absorbed radiation energy) is probably the radiation quantity that most closely correlates with potential radiation damage during a diagnostic procedure. This is because it reflects not only the concentration of the radiation absorbed in the tissue but also the amount of tissue affected by the radiation.

  There is no practical method for measuring integral dose in the human body. However, since most of the radiation energy delivered to a body is absorbed, the integral dose can be estimated to within a few percent from the total energy delivered to the body.

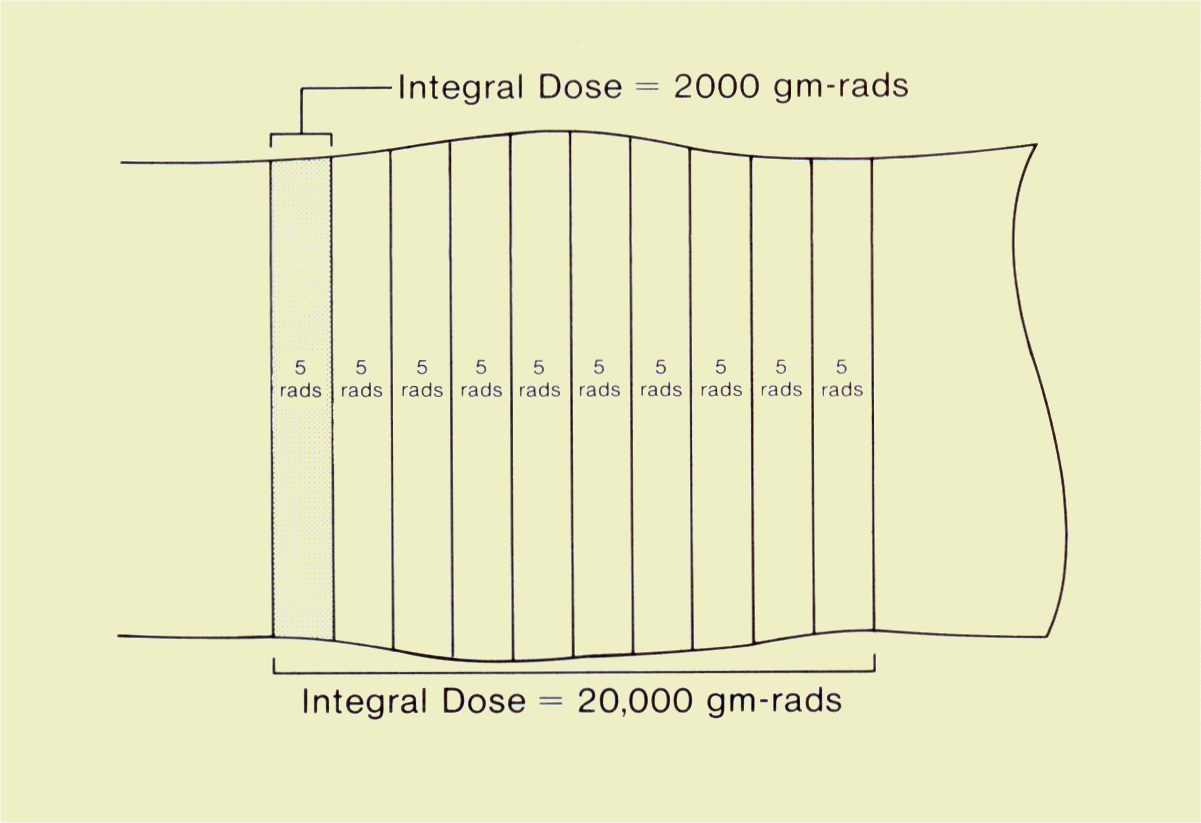
  Computed tomography can be used to demonstrate integral dose, as illustrated below. We begin with a one-slice examination and assume that the average dose to the tissue in the slice is 5 rad. If there are 400 g of tissue in the slice, the integral dose will be 2,000 gram-rad. If we now perform an examination of 10 slices, but all other factors remain the same, the dose (energy concentration) in each slice will remain the same. However, the integral dose (total energy) increases in proportion to the number of slices and is now 20,000 gram-rad. In this example we made the simplifying assumption that no radiation is scattered from one slice to another. In reality, some radiation is exchanged between contiguous slices but that does not affect the concept presented.

Dose Length Product (DLP)

CONTENTS

The Concept of Dose Length Product

   We recall that the CTDI is the practical quantity for specifying dose in CT procedures.  The associated quantity for specifying the "total radiation" to a patient is the dose length product (DLP) as illustrated here.

   The DLP is just the product of the CTDI value and the length of the body area scanned.  It has the units of either rad-cm or Gy-cm.  It is a useful and practical quantity for comparing the total radiation to  patients for various CT procedures.  It is, however, not a precise measure of the total radiation or integral dose; that is more difficult to determine.

BIOLOGICAL IMPACT

CONTENTS

  It is sometimes desirable to express the actual or relative biological impact of radiation. It is necessary to develop a distinction between the biological impact and the physical quantity of radiation because all types of radiation do not have the same potential for producing biological change. For example, one rad of one type of radiation might produce significantly more radiation damage than one rad of another type. In other words, the biological impact is determined by both the quantity of radiation and its ability to produce biological effects. Two radiation quantities are associated with biological impact.

   Dose Equivalent

CONTENTS

  Dose equivalent (H) is the quantity commonly used to express the biological impact of radiation on persons receiving occupational or environmental exposures. Personnel exposure in a clinical facility is often determined and recorded as a dose equivalent.

  Dose equivalent is proportional to the absorbed dose (D), the quality factor (Q), and other modifying factors (N) of the specific type of radiation. Most radiations encountered in diagnostic procedures (x-ray, gamma, and beta) have quality and modifying factor values of 1. Therefore, the dose equivalent is numerically equal to the absorbed dose. Some radiation types consisting of large (relative to electrons) particles have quality factor values greater than 1. For example, alpha particles have a quality factor value of approximately 20.

  The conventional unit for dose equivalent is the rem, and the Sl unit is the sievert (Sv). When the quality factor is 1, the different relationships between dose equivalent (H) and absorbed dose (D) are

H(rem) = D(rad)

H(Sv) = D(Gy).

  Dose equivalent values can be converted from one system of units to the other by:

1 Sv = 100 rem.

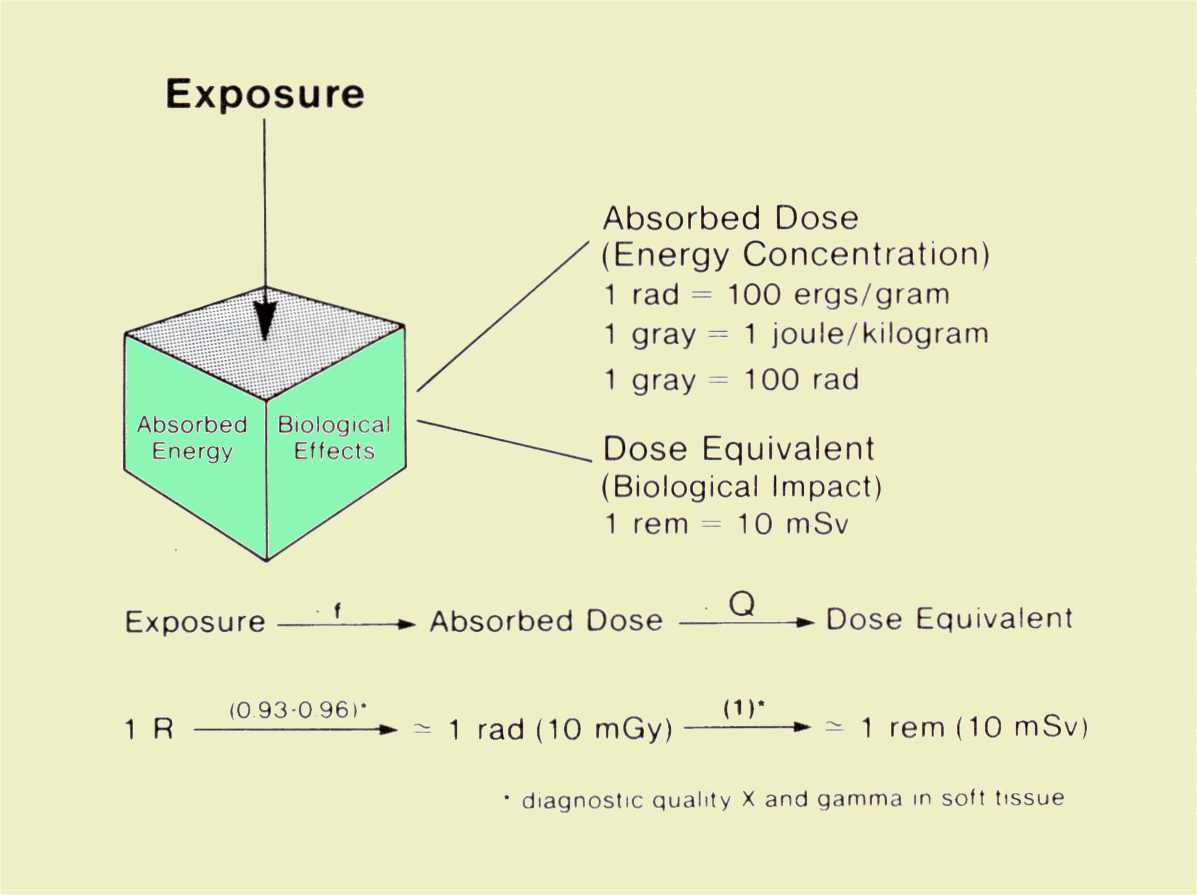
  The figure below is a summary of the general relationship among the three quantities: exposure, absorbed dose, and dose equivalent. Although each expresses a different aspect of radiation, they all express radiation concentration. For the types of radiation used in diagnostic procedures, the factors that relate the three quantities have values of approximately 1 in soft tissue. Therefore, an exposure of 1 R produces an absorbed dose of approximately 1 rad, which, in turn, produces a dose equivalent of 1 rem.

Relationship of Exposure, Absorbed Dose, and Dose Equivalent

Relative Biological Effectiveness

CONTENTS

  When specific radiation effects rather than general risk are being considered, the relative biological effectiveness (RBE) of the radiation must be taken into account. The value of the RBE depends on characteristics of the radiation and the specific biological effects being considered. This radiation characteristic is generally not used in association with diagnostic procedures. Additional discussions of the concept can be found in radiation biology texts.

Effective Dose

CONTENTS

The Concept of Effective Dose

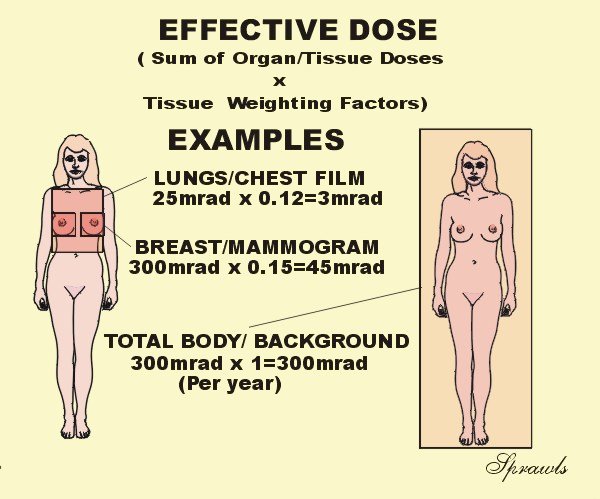
   Effective dose is becoming a very useful radiation quantity for expressing relative risk to humans, both patients and other personnel.  It is actually a simple and very logical concept.  It takes into account the specific organs and areas of the body that are exposed.  The point is that all parts of the body and organs are not equally sensitive to the possible adverse effects of radiation, such as cancer induction and mutations.

   For the purpose of determining effective dose, the different areas and organs have been assigned tissue weighting factor (w_T) values.  For a specific organ or body area the effective dose is:

Effective Dose (Gy) = Absorbed Dose (Gy) x w_T

   If more than one area has been exposed, then the total body effective dose is just the sum of the effective doses for each exposed area.  It is a simple as that.  Now let's see why effective dose is such a useful quantity.  There is often a need to compare the amount of radiation received by patients for different types of x-ray procedures, for example, a chest radiograph and a CT scan.  The effective dose is the most appropriate quantity for doing this.  Also, by using effective dose it is possible to put the radiation received from diagnostic procedures into perspective with other exposures, especially natural background radiation.

LIGHT

CONTENTS

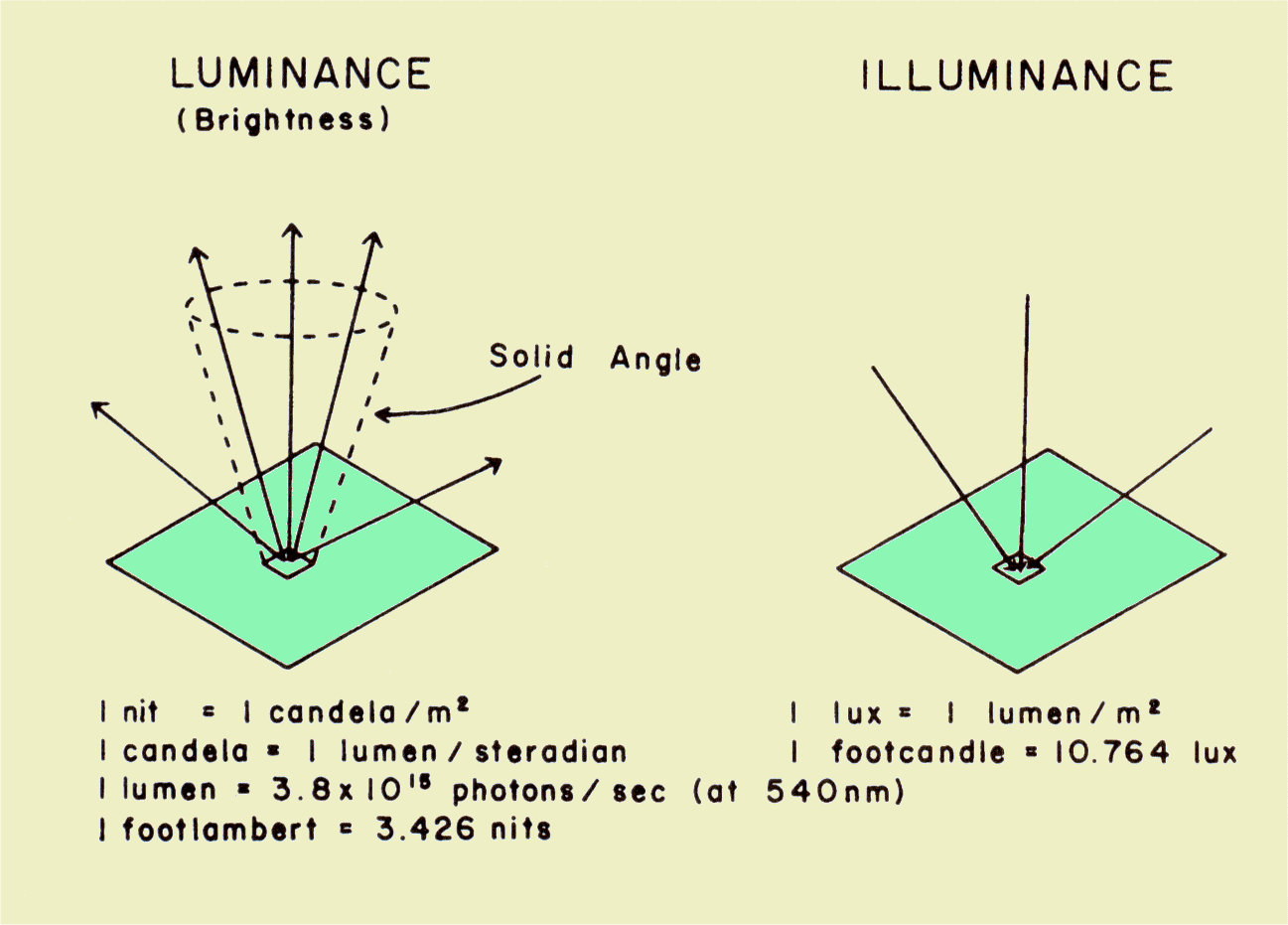
The basic light quantities and units encountered in radiology can be conveniently divided into two categories: those that express the amount of light emitted by a source and those that describe the amount of light falling on a surface, such as a piece of film. The relationships of several light quantities and units are shown below.

Light Quantities and Units Encountered in Radiology

Luminance

CONTENTS

Luminance is the light quantity generally referred to as brightness. It describes the amount of light being emitted from the surface of the light source. The basic unit of luminance (brightness) is the nit, which is equivalent to 1 candela per m² of source area.

The concept of luminance is somewhat easier to understand if it is related to the number of light photons involved. The quantity for specifying an amount of light is the lumen. One lumen of light with wavelengths encountered in x-ray imaging systems (540 nm) is equivalent to 3.8 x 10¹⁵ photons per second. Another factor that determines luminance is the concentration of light in a given direction. This can be described in terms of a cone or solid angle that is measured in units of steradians (sr).

If a light source produces an intensity of 1 cd/m² of surface area, it has a luminance of 1 nit. Perhaps it is more realistic to consider the quantity of light that would be emitted from a 1-mm² area of a source, such as the output screen of an image intensifier. One millimeter square is 10^-6 m². If the intensifier has a luminance (brightness) of 1 nit, the intensity from an area of 1 mm² would be 10^-6 lumen in a 1-unit solid angle. This would be equivalent to 3.8 x 10⁹ photons per second, leaving the 1-mm² area through a cone (solid angle) of 1 sr of source area.

Viewbox and other image display device brightness is measured in the units of nits. It is generally in the range of 1,500 nits to 2,000 nits for most image viewing except mammography, where it should be at least 3,500 nits.

Another unit used for specifying luminance is the foot-lambert, which is equivalent to 3.426 nits.

  Illuminance

CONTENTS

Illuminance is a specification of the quantity of light falling on or illuminating a surface. The basic unit is the lux. A surface has an illuminance of 1 lux when it receives 1 lumen/m² of surface area. Consider a small area on a piece of film that is 1 mm². For light with a wavelength of 540 nm, there are 3.8 x 10¹⁵ photons per second per lumen. An illuminance to the film of 1 lux would be equivalent to 3.8 x 10² photons per sec to a 1-mm² area. The total light exposure to a film is found by multiplying the illuminance, in lux, by the exposure time, in seconds, and is expressed in units of lux-seconds.

Another unit used in some literature for specifying illuminance is the footcandle, which is equivalent to 10.764 lux.

RADIO FREQUENCY RADIATION

CONTENTS

Radio frequency (RF) radiation is used in magnetic resonance imaging (MRI). During an imaging procedure, pulses of RF energy are applied to the patient's body where most of it is absorbed. Conventional energy units are used to express the amount of RF energy imparted to the body.

Power is the rate at which energy is transferred. The unit for power is the watt, which is equivalent to an energy transfer at the rate of 1 joule/second. During the acquisition phase of MRI, the system transfers energy to the patient's body at some specific power level. The actual power (watts) used depends on many factors associated with the examination.

Specific Absorption Rate (SAR)

CONTENTS

From the standpoint of effect on the patient's body a more significant quantity is the concentration of power in the tissue. This is expressed in the units of watts per kilogram of tissue and is designated the specific absorption rate (SAR). Since RF energy is not uniformly distributed within the body, two quantities must be considered: the SAR in a specific location and the average SAR within the total body. The RF energy absorbed by the tissue is converted into heat. Therefore, the power concentration is an indication of the rate at which heat is produced within specific tissue.