|
|
|
CONTENTS |
|
One of the characteristics of x- and gamma radiations that makes them useful for medical imaging is their penetrating ability. When they are directed into an object, some of the photons are absorbed or scattered, whereas others completely penetrate the object. The penetration can be expressed as the fraction of radiation passing through the object. Penetration is the inverse of attenuation. The amount of penetration depends on the energy of the individual photons and the atomic number, density, and thickness of the object, as illustrated
below.
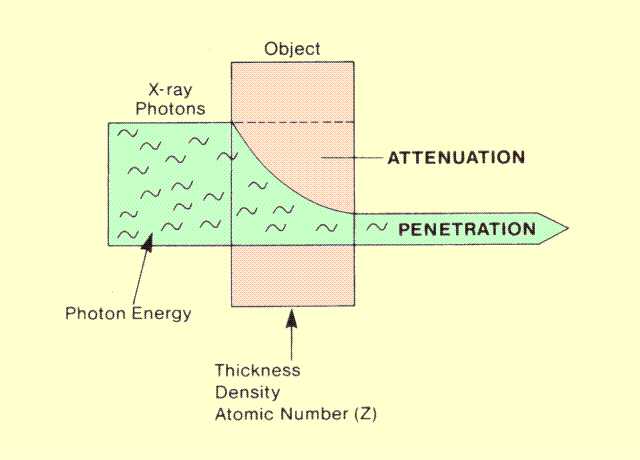
Factors That Affect the Penetration of Radiation through a Specific Object
The probability of photons interacting, especially with the photoelectric effect, is related to their energy. Increasing photon energy generally
decreases the probability of interactions (attenuation) and,
therefore, increases penetration. As a rule, high-energy photons are more
penetrating than low-energy photons, although there are limits and exceptions to this, which we discuss later.
|
|
|
|
CONTENTS |
|
It might be helpful in understanding the characteristics of radiation penetration to first consider the range, or distance, traveled by the individual photons before they are absorbed or scattered. When photons enter an object, they travel some distance before interacting. This distance can be considered the range of the individual photons.
A characteristic of radiation is that all photons do not have the same range, even when they have the same energy. In fact, there is no way to predict the range of a specific photon. Let us consider a group of mono-energetic photons entering an object, as shown
below. Some of the photons travel a relatively short distance before interacting, whereas others pass through or penetrate the object. If we count the number of photons penetrating through each thickness of material, we begin to see a fundamental characteristic of photon penetration. The relationship between the number of photons reaching a specific point and the thickness of the material to that point is exponential.
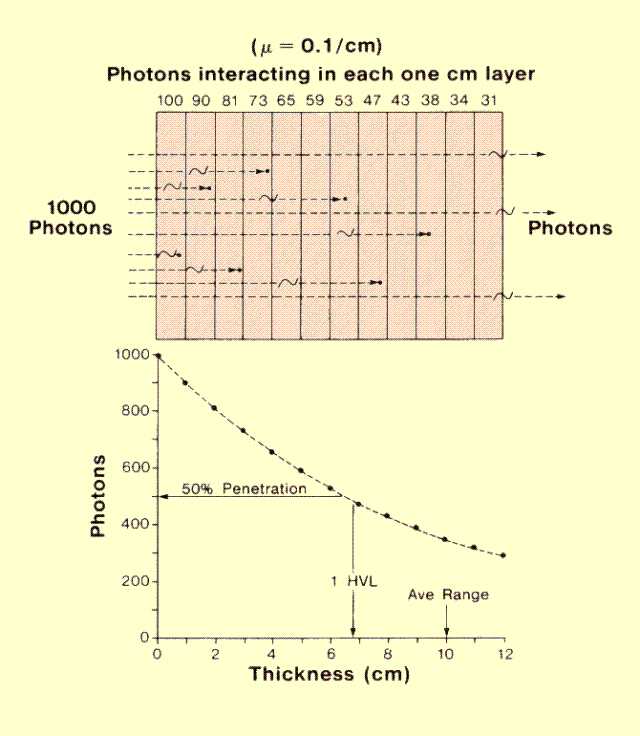
Penetration Range of Individual Photons
The nature of the exponential relationship is that each thickness of material attenuates the same fraction of photons entering it. This means that the first layer encountered by the radiation beam attenuates many more photons than the succeeding layers.
In a given situation a group of photons have different individual ranges which, when considered together, produce an average range for the group. The average range is the average distance traveled by the photons before they interact. Very few photons travel a distance exactly equal to the average range. The average range of a group of photons is inversely related to the attenuation rate. Increasing the rate of attenuation by changing photon energy or the type of material decreases the average range of photons. Actually, the average photon range is equal to the reciprocal of the attenuation coefficient (µ):
Average Range (cm) =1/Attenuation Coefficient (cm-1)
Therefore, the average distance (range) that photons penetrate a material is determined by the same factors that affect the rate of attenuation: photon energy, type of material (atomic number), and material density.
Average photon range is a useful concept for visualizing the penetrating characteristics of radiation photons. It is, however, not the most useful parameter for measuring and calculating the penetrating ability of radiation.
|
|
|
|
CONTENTS |
|
Half value layer
(HVL) is the most frequently used quantity ore factor for describing both the penetrating ability of specific radiations and the penetration through specific objects. HVL is the thickness of material penetrated by one half of the radiation and is expressed in units of distance (mm or cm).
Increasing the penetrating ability of a radiation increases its
HVL. HVL is related to, but not the same as, average photon range. There is a difference between the two because of the exponential characteristic of x-ray attenuation and penetration. The specific relationship is
HVL = 0.693 X Average Range = 0.693/µ.
This shows that the HVL is inversely proportional to the attenuation coefficient. The number, 0.693, is the exponent value that gives a penetration of 0.5:
(e-0.693 = 0.5).
Any factor that changes
the rate of interactions and the value of the attenuation coefficient also changes the HVL. These two quantities are compared for aluminum in the figure below. Aluminum has two significant applications in an x-ray system. It is used as a material to filter x-ray beams and
also as a reference material for measuring the penetrating ability
(HVL) of x-rays. The value of the attenuation coefficient decreases rather rapidly with increased photon energy and causes the penetrating ability to increase.
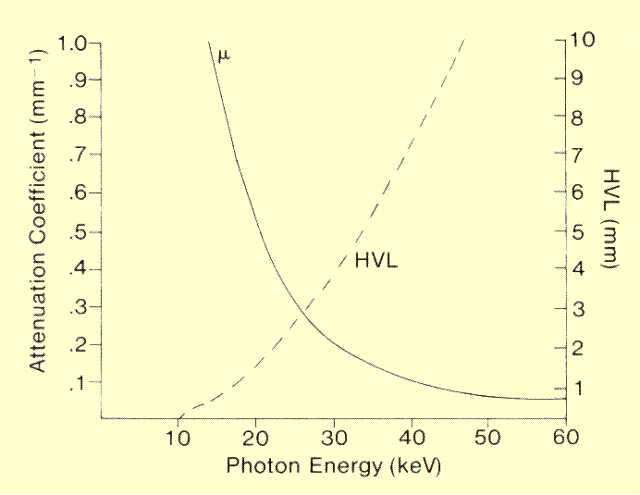
Relationship between Attenuation Coefficient and HVL for Aluminum
The figure
below illustrates an important aspect of the HVL concept. If the penetration through a thickness of 1 HVL is 0.5 (50%), the penetration through a thickness of 2 HVLs will be 0.5 x 0.5 or 25%. Each succeeding layer of material with a thickness of 1 HVL reduces the number of photons by a factor of 0.5. The relationship between penetration (P) and thickness of material that is n half value layers thick is
P = (0.5 )n.
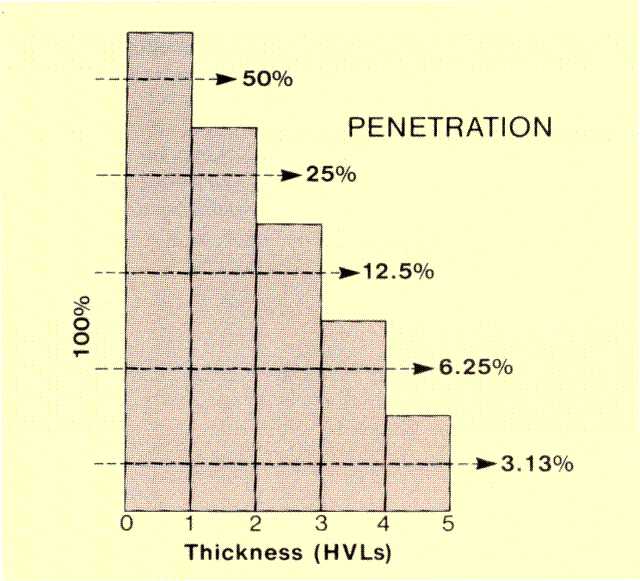
Relationship between Penetration and Object Thickness Expressed in HVLs
An example using this relationship is determining the penetration through lead shielding. Photons of 60 keV have an HVL in lead of 0.125 mm. The problem is to determine the penetration through a lead shield that is 0.5 mm thick. At this particular photon energy, 0.5 mm is 4
HVLs, and the penetration is
n =
thickness / HVL = 0.5 / 0.125 = 4
P =
(0.5)4 = 0.0625.
The following
figure summarizes two important characteristics of
HVL. In a specific material, the HVL is affected by photon energy. On the other hand, for a specific photon energy, the thickness of 1 HVL is related to characteristics of the material, density, and/or atomic number.
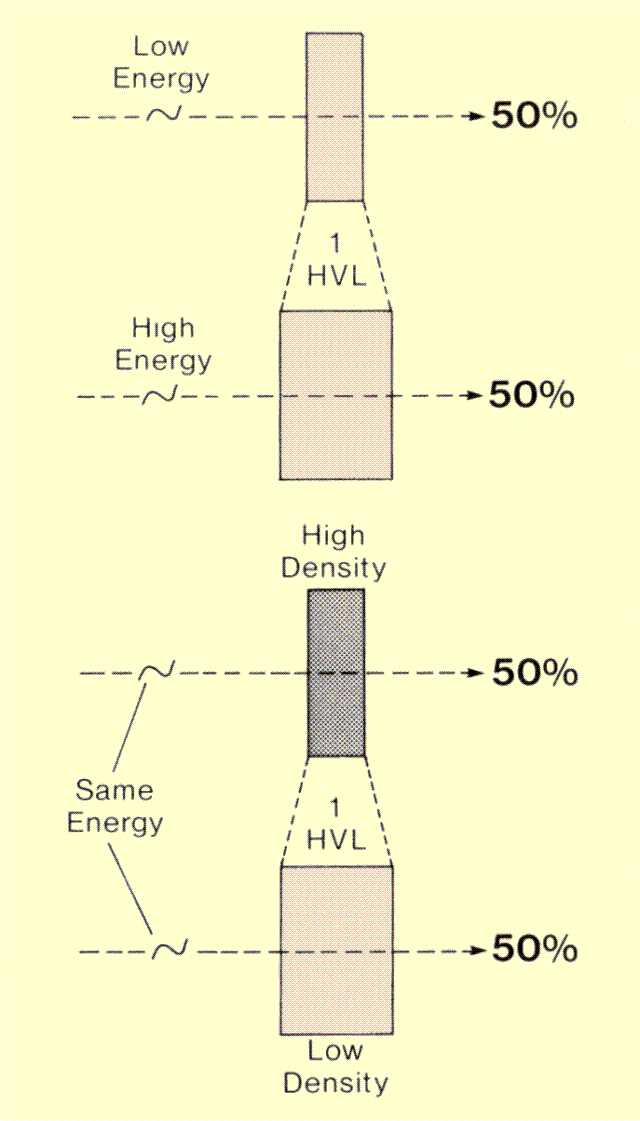
Factors That Affect the Thickness of 1 HVL
The general procedure for determining the HVL value of an x-ray beam is illustrated
below. Two items are required. One is an instrument for measuring radiation exposure, and the second is a set of aluminum absorbers. Typically, the set includes absorbers with thicknesses of both 0.5 mm and 1 mm.
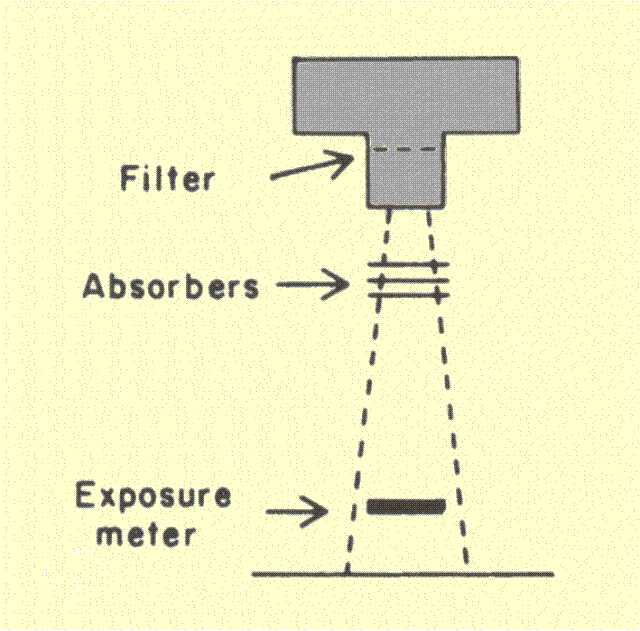
Procedures for Determining the HVL of an X-Ray Beam
The exposure meter is positioned as shown, and a reading is made. Aluminum absorbers are then placed in the beam, typically in 0.5- or 1-mm increments, and an exposure reading is made. Dividing each exposure reading by the exposure with no absorber gives the penetration for each thickness of absorber. The penetration values are then plotted as a function of aluminum-absorber thickness. The absorber thickness corresponding to a penetration value of 0.5
(50%) is the HVL. This value is referred to as the first HVL. The second HVL value is the additional thickness required to reduce the penetration to 0.25. Generally, it is larger than the first value because the first aluminum absorbers added to the beam act as a filter and produce an increase in the equivalent energy and corresponding HVL value. In actual practice, it is usually more desirable to plot the penetration values on a logarithmic scale (by using semi-logarithmic graph paper) so that the resulting graph is essentially a straight line.
|
|
|
|
|
|
CONTENTS |
|
The general term "quality" refers to an x-ray beam's penetrating ability. It has been shown that, for a given material, the penetrating ability of an x-ray beam depends on the energy of the photons. Up to this point, the discussion has related penetration to specific photon energies. For x-ray beams that contain a spectrum of photon energies, the penetration is different for each energy. The overall penetration generally corresponds to the penetration of a photon energy between the minimum and maximum energies of the spectrum. This energy is designated the
effective energy of the x-ray spectrum as shown
below. The effective energy of an x-ray spectrum is the energy of a mono-energetic beam of photons that has the same penetrating ability (HVL) as the spectrum of photons.
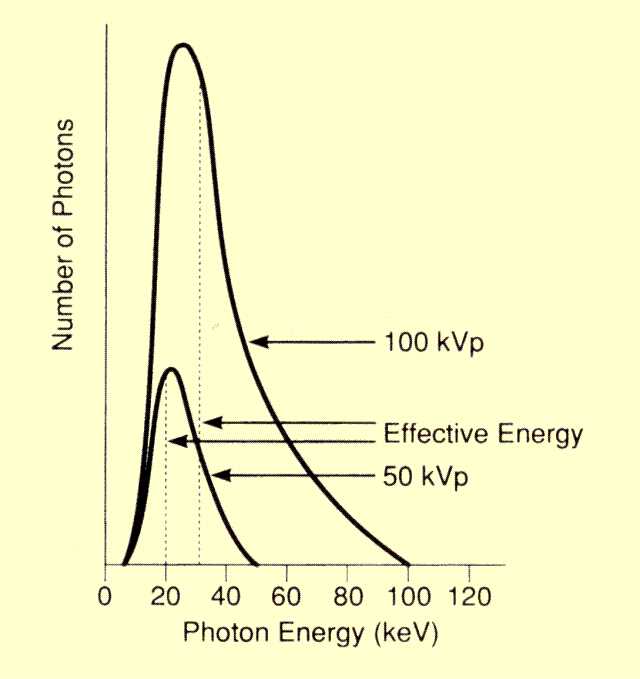
Effective Energy of X-Ray Spectra
The effective energy is generally close to 30% or 40% of peak energy, but its exact value depends on the shape of the spectrum. For a given
KV, two factors that can alter the spectrum are the amount of filtration in the beam and the high voltage waveform used to produce the x-rays.
|
|
|
|
CONTENTS |
|
As an x-ray beam made up of different photon energies passes through many materials, photons of certain energies penetrate better than others. This selective attenuation of photons, according to their energy, is referred to as filtration.
The figure below shows the penetration through two materials of special interest, a 1-cm thickness of muscle and a 1-mm thickness of aluminum. The penetration through the muscle, or soft tissue, is considered first. For photons with energies less than 10 keV, there is virtually no penetration; all the photons are attenuated by the tissue. The low penetration in tissue by photons of this energy is because of the high value for the attenuation coefficient. Recall that the high attenuation coefficient value is the result of photoelectric interactions, which are highly probable at this energy. In the range of 10 keV to 25 keV, penetration rapidly increases with energy. As photon energy increases to about 40 keV, penetration increases, but much more gradually. Of special interest is the very low penetrating ability of x-ray photons with energies below approximately 20 keV. At this energy, the penetration through 1 cm of tissue is 0.45, and the penetration through 15 cm of tissue is;
P = (0.45)15 = 0.0000063.
On the other hand, the penetration through 15 cm of tissue for photons with an energy of 50 keV is
P = (0.8)15 = 0.035.
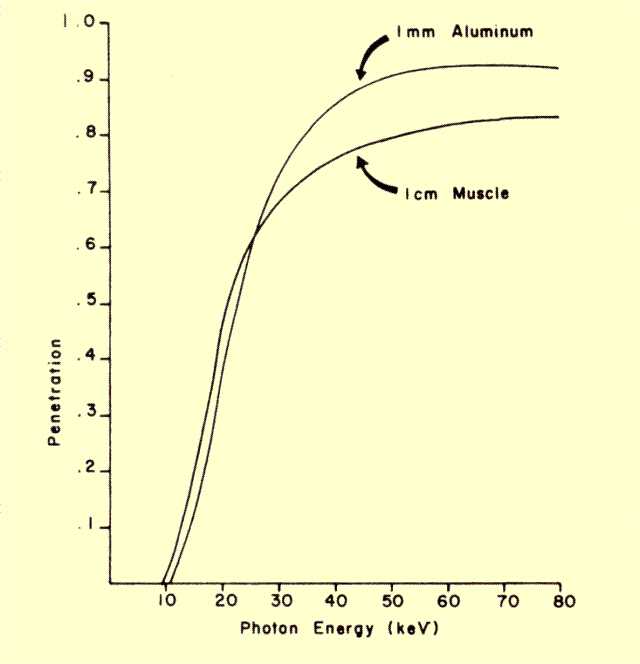
Penetration of Soft Tissue and Aluminum for Various Photon Energies
A significant portion (3.5%) of photons with an energy near 50 keV penetrate a 15-cm-thick patient, whereas virtually no photons with energies of 20 keV or less make it through. This means that low-energy photons in an x-ray spectrum do not contribute to image formation; they contribute only to patient exposure. In other words, the tissue of the body selectively filters out the low-energy photons.
An obvious solution is to place some material in the x-ray beam, before it enters the patient, to filter out the low-energy photons. In diagnostic x-ray equipment, aluminum is normally used for this purpose.
The figure above shows the penetration through a 1-mm thickness of aluminum. Typically, most x-ray machines contain the equivalent of several millimeters of aluminum filtration. This might not always be in the form of aluminum because several objects contribute to x-ray beam filtration: the x-ray tube window, the x-ray beam collimator mirror, and the table top in fluoroscopic equipment. The total amount of filtration in a given x-ray machine is generally specified in terms of an equivalent aluminum thickness.
The addition of filtration significantly alters the shape of the x-ray spectrum, as shown
below. Since filtration selectively absorbs the lower energy photons, it produces a shift in the effective energy of an x-ray beam.
The figure below compares an unfiltered spectrum to spectra that passed through 1-mm and 3-mm filters. It is apparent that increasing the filtration from 1 mm to 3 mm of aluminum produces a noticeable decrease in the number of x-ray photons. It should be observed, however, that most of this decrease is in photons with energies less than approximately 40 keV. These are the photons with a low probability of penetrating a typical patient and contributing to image formation. They do, however, contribute to patient exposure.
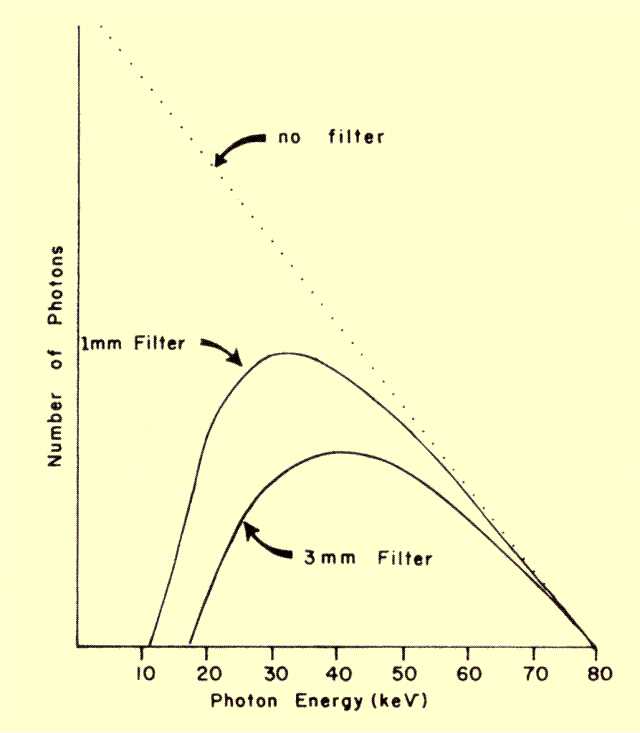
X-Ray Spectra After Filtration
Adding filtration increases the penetration (HVL) of an x-ray beam by removing the low-energy photons. HVL values are used to judge the adequacy of the filtration. Regulations that specify filtration requirements generally state a minimum acceptable HVL value. Typical values are shown in
the table below. It is assumed that if an x-ray beam has the minimum specified HVL value at a stated
KV, the filtration is adequate.
Recommended Minimum Penetration (HVL) for Various
KV Values
| KV |
Minimum
penetration (HVL)
for
Aluminum (mm) |
|
30 |
0.3 |
|
50 |
1.2 |
|
70 |
1.5 |
|
90 |
2.5 |
|
110
|
3.0 |
|
|
|
|
CONTENTS |
|
Up to this point, the x-ray photons that penetrate an object were assumed to be those that had escaped both photoelectric and Compton interactions. In situations in which Compton interactions are significant, it is necessary to modify this concept because some of the radiation removed from the primary beam by Compton interactions is scattered in the forward direction and creates the appearance of increased penetration. A prime example is an x-ray beam passing through the larger portions of the human body, as illustrated
below. When significant forward-scattered radiation combines with the penetrated portion of the primary beam, the effective penetration, Pe, is given by:
Pe=P x S
where S is the scatter factor. Its value ranges from 1 (no scatter) to approximately 6 for conditions encountered in some diagnostic examinations.
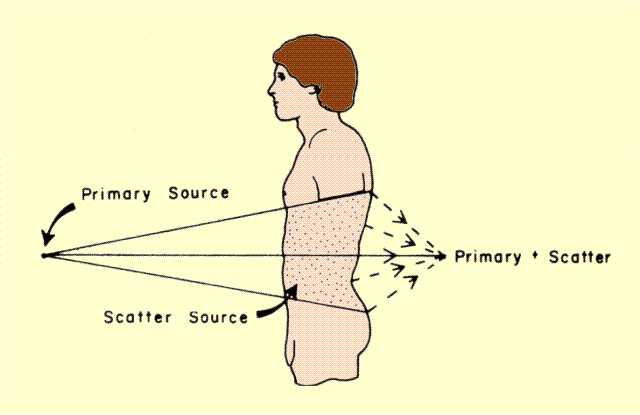
Scattered Radiation Adds to the Primary Radiation That Penetrates an Object
Several factors contribute to the amount of radiation scattered in the forward direction and hence to the value of S. One of the most significant factors is the x-ray beam area, or field size. Since the source of the scattered radiation is the volume of the patient within the primary x-ray beam, the source size is proportional to the beam area. Within limits, the value of S increases from a value of 1
(no scatter), more or less, in proportion to field size. Another important factor is body section thickness, which affects the size of the scattered radiation source. A third significant factor is
KV. As the KV is increased over the diagnostic range, several changes occur. A greater proportion of the photons that interact with the body are involved in Compton interactions, and a greater proportion of the photons created in Compton interactions scatters in the forward direction. Perhaps the most significant factor is that the scattered radiation produced at the higher
KV values is more penetrating. A larger proportion of it leaves the body before being absorbed. When the scattered radiation is more penetrating, there is a larger effective source within the patient. At low
KV values, most of the scattered radiation created near the entrance surface of the x-ray beam does not penetrate the body; at higher
KV values, this scattered radiation contributes more to the radiation passing through the body.
|
|
|
|
CONTENTS |
|
We have seen that the amount of radiation that penetrates through a specific thickness of material is determined by the energy of the individual photons and the characteristics (density and atomic number) of the material. HVL values provide useful information about the penetration of a specific radiation in a specific material. When an HVL value is known, the penetration through other thicknesses can be easily determined.
The table below gives HVL values for several materials related to diagnostic imaging.
HVL Values for Certain Materials
|
Material
|
HVL (mm)
|
| 30 keV |
60 keV |
120 keV |
| Tissue |
20.0 |
35.0 |
45.0 |
| Aluminum |
2.3 |
9.3 |
16.6 |
| Lead |
0.02 |
0.13 |
0.15 |
|
|
| | |











