|
|
|
CONTENTS |
|
One of the most important quantities associated with a sample or collection of radioactive material is its activity. Activity is the rate at which the nuclei within the sample undergo transitions and can be expressed in terms of the number of transitions per second (tps). Two units are used: the becquerel (Bq), equivalent to 1 tps, and the curie (Ci), equivalent to 3.7 x
1010 tps. The becquerel is an Sl unit. The curie was first introduced as the activity of 1 g of radium. However, it was later discovered that the activity of 1 g of radium is not exactly 1 Ci, although the number of transitions per second per curie remains the same. Some useful conversions are
1 Ci = 3.7 x 1010 Bq
1 mCi = 37 MBq
1 MBq = 27 ÁCi.
The activity of a sample is related to two quantities used in clinical nuclear medicine. These are illustrated
below and are (1) the number of radioactive (untransformed) nuclei in the sample and (2) the elapsed time. Both relationships involve the lifetime of the radioactive material. The lifetime is the time between the formation of a radioactive nucleus and its radioactive transition.
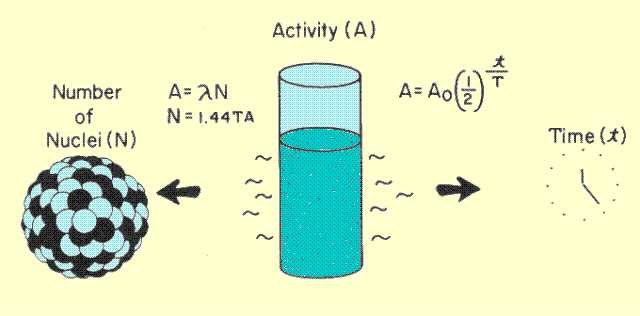
Relationship of Activity to Number of Nuclei and Elapsed Time
|
|
|
|
CONTENTS |
|
A fundamental characteristic of radioactivity is that all nuclei, even of the same radioactive nuclide, do not have the same lifetime. This is illustrated
below. There is no way to determine or predict the lifetime of a nucleus. However, we can determine the average lifetime of the nuclei of a specific radioactive nuclide. The average lifetime is a unique characteristic of each specific nuclide.
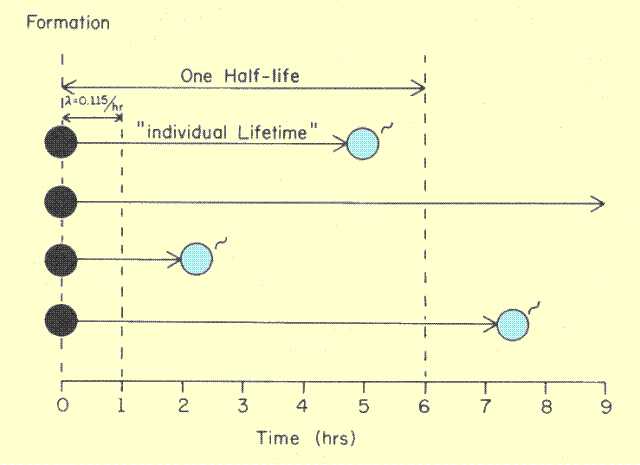
Variations in Lifetimes of Radioactive Nuclei
|
|
|
|
CONTENTS |
|
It is generally more useful to express the lifetime of a radioactive material in terms of the half-life.
T1/2, rather than the average life,
Ta. The half-life is the time required for one-half of the nuclei to undergo transitions. The half-life is shorter than the average life. The specific relationship is
T1/2 = 0.693
Ta,
or
Ta = 1.44
T1/2.
Since half-life is proportional to the average life, the value is specific for each radionuclide. The half-lives for many nuclides of interest are given in Table 5-1 of Chapter 5.
|
|
|
|
CONTENTS |
|
Another way to express the lifetime characteristic of a radioactive substance is by means of the transformation constant, delta, often referred to as the decay constant. The transformation constant actually expresses the probability that a nucleus will undergo a transition in a stated period of time. In the example in
the figure above, the value of the transformation constant is 0.115 per hour. This means that a nucleus has a probability of 0.115 or an 11.5% chance of undergoing a transition in 1 hour. The value of the transformation constant is inversely related to lifetime. The probability of undergoing a transition in 1 hour is obviously much less for a radionuclide with a long lifetime (half-life). The actual relationship between the transformation constant and lifetime is:
T1/2 =
0.693/l .
The number, 0.693, is the natural logarithm of the number two, and frequently appears in relationships involving half-life. The transformation constant,
l,
is the reciprocal of the average life, Ta:
l
= 1/Ta .
We can summarize the lifetime characteristics of a radioactive substance: The lifetimes of nuclei within a sample vary tremendously. For a specific radioactive substance or nuclide, however, a characteristic lifetime can be expressed in terms of half-life, average life, or the transformation constant. If the value for one term is known, the others can be derived using the simple relationships above.
|
|
|
|
CONTENTS |
|
Although activity does not express the amount of radioactive material present, it is proportional to the amount present at a specific time. The amount can be expressed by quantities such as mass, volume, or number of nuclei. We now consider the relationship of activity and the number of nuclei, N, in a specific sample.
We have just seen that transitions are spread over a longer time for some nuclides than for others. In other words, for a given number of radioactive nuclei, the rate of transition (activity) is inversely related to the lifetime of the nuclide. The transformation constant, lambda, can be used to relate the activity to the number of nuclei in a sample. When applied to a large number of nuclei, the value of the transformation constant represents the fraction or percentage of the nuclei that will undergo a transition during one unit of time. Suppose we have a sample containing one million radioactive nuclei and the transformation constant has a value of 0.001 per second.
Activity = l x N
= (0.001/s)(1,000,000)
= 1,000 transitions/second.
We should emphasize the difference between activity and amount of radioactive material, or number of nuclei. Both quantities are important when using radionuclides for clinical purposes. The amount of radioactive material is the quantity of radioactive nuclei or atoms in a sample, whereas the activity is the rate at which they are undergoing transitions and emitting radiation. Although activity is proportional to the number of nuclei, the proportion varies from one nuclide to another depending on its lifetime. From the relationships above, it can be seen that for a given quantity of radioactive material, activity is inversely related to half-life:
Activity = 0.693 x N / T1/2
Number of nuclei = 1.44 x Activity x T1/2.
A relatively small amount of radioactive material can have the same activity as a larger amount if the smaller quantity has a shorter lifetime (half-life).
|
|
|
|
CONTENTS |
|
The quantity of radioactive nuclei that undergo transitions in a period of time is usually designated the cumulated activity, ├, and is expressed in the units of microcurie-hours. 1 ÁCi-hr is equivalent to 133 million (13.3 x
107) transitions.
The relationship between cumulated activity, ├, and the initial activity of a collection of radioactive material, A, is
├ (mCi-hr) = 1.44 x A
(mCi) x
T1/2 (hr).
The quality of nuclear radiation images is generally related to activity, whereas patient dose is more dependent on the amount of radioactive material or cumulated activity. Therefore, the "ratio" of image quality to patient dose is inversely proportional to radionuclide lifetime (half-life); a radionuclide with a short half-life yields more activity from less radioactive material and is generally desirable for clinical studies. The relationship of patient dose to half-life (and other factors) is explored in a later chapter.
|
|
|
|
CONTENTS |
|
One of the most important characteristics of a radioactive material is that the quantity and activity constantly change with time. As each nucleus undergoes transition, it no longer belongs to the radioactive material. In each transition one atom is removed from the parent radioactive material and converted into the daughter product. Because the activity is proportional to the quantity of radioactive material at any instant in time, both quantity and activity decrease continuously with elapsed time. This decrease is generally referred to as radioactive decay.
The nature of radioactive decay is such that during a given time interval the same fraction (or percent) of radioactive nuclei will undergo transitions. The important point is that the fraction (but not the amount) per unit time remains constant. The fraction of nuclei that undergo transitions in a specified time period is different for each nuclide and depends on the nuclide lifetime (transformation constant or half-life). This characteristic of radioactive decay is illustrated
below.
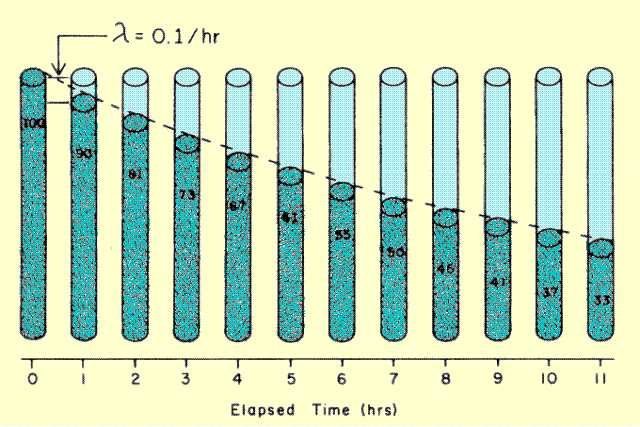
Relationship between Amount of Radioactive Material and Elapsed Time
Let us assume that we have a radioactive material with a transformation constant of 0.1 per hour. This means that approximately one-tenth of the nuclei will undergo transitions during a 1-hour time interval. If we begin with 100 units of radioactive material, 10 units will undergo transition during the first hour. At the beginning of the second hour there will be 90 units of material. During the second hour, one-tenth of 90 units will undergo transition which results in 81 units remaining at the end of the second hour. The relationship between amount of radioactivity and time is not linear, but is exponential. This relationship is encountered when the fraction of material undergoing change remains constant, but the amount decreases with time.
|
|
|
|
CONTENTS |
|
It is often necessary to determine the fraction of radioactive material (or activity) that remains after a specific elapsed time. If the elapsed time is one half-life, the remaining fraction, f, is always 0.5 . If the elapsed time is not one half-life, the remaining fraction is the fraction 0.5 multiplied by itself the number of times corresponding to the number of half-lives. For example,
1 half-life, f = 0.5
2 half-lives, f = (0.5) x (0.5) = 0.25
3 half-lives, f = (0.5) x (0.5) x (0.5) = 0.125
4 half-lives, f = (0.5) x (0.5) x (0.5) x (0.5) = 0.0625.
This can be expressed as
f = (0.5)t/T =
(0.5)n
where t is the elapsed time, T is the half-life, and n is the number of half-lives. When the elapsed time is an integral number of half-lives, the remaining fraction can be easily calculated. If the elapsed time is not an integral number of half-lives, the computation requires a calculator that can perform exponential functions or a special mathematical table.
The following table gives the remaining fractions for several elapsed time intervals expressed in terms of the number of half-lives.
Tabulation of Remaining Fraction (f) After an
Elapsed Time of n Half Lives
| n |
f |
|
n |
f |
|
n |
f |
| 0.0 |
1.0 |
|
1.25 |
0.42 |
|
2.5 |
0.175 |
| 0.05 |
0.97 |
|
1.3 |
0.42 |
|
2.55 |
0.17 |
| 0.1 |
0.93 |
|
1.35 |
0.39 |
|
2.6 |
0.165 |
| 0.15 |
0.90 |
|
1.4 |
0.38 |
|
2.65 |
0.16 |
| 0.2 |
0.87 |
|
1.45 |
0.37 |
|
2.7 |
0.15 |
| 0.25 |
0.84 |
|
1.5 |
0.35 |
|
2.75 |
0.145 |
| 0.3 |
0.81 |
|
1.55 |
0.34 |
|
2.8 |
0.14 |
| 0.35 |
0.78 |
|
1.6 |
0.33 |
|
2.85 |
0.135 |
| 0.4 |
0.76 |
|
1.65 |
0.32 |
|
2.9 |
0.13 |
| 0.45 |
0.73 |
|
1.7 |
0.31 |
|
2.95 |
0.129 |
| 0.5 |
0.71 |
|
1.75. |
0.3 |
|
3.0 |
0.125 |
| 0.55 |
0.68 |
|
1.8 |
0.29 |
|
3.5 |
0.088 |
| 0.6 |
0.66 |
|
1.85 |
0.28 |
|
4.0 |
0.063 |
| 0.65 |
0.64 |
|
1.9 |
0.27 |
|
4.5 |
0.044 |
| 0.7 |
0.62 |
|
1.95 |
0.26 |
|
5.0 |
0.031 |
| 0.75 |
0.59 |
|
2.0 |
0.25 |
|
5.5 |
0.022 |
| 0.8 |
0.57 |
|
2.05 |
0.24 |
|
6.0 |
0.016 |
| 0.85 |
0.55 |
|
2.1 |
0.23 |
|
6.5 |
0.011 |
| 0.9 |
0.54 |
|
2.15 |
0.225 |
|
7.0 |
0.008 |
| 0.95 |
0.52 |
|
2.2 |
0.22 |
|
7.5 |
0.006 |
| 1.0 |
0.50 |
|
2.25 |
0.21 |
|
8.0 |
0.004 |
| 1.05 |
0.48 |
|
2.3 |
0.2 |
|
8.5 |
0.003 |
| 1.1 |
0.47 |
|
2.35 |
0.195 |
|
9.0 |
0.002 |
| 1.15 |
0.45 |
|
2.4 |
0.19 |
|
9.5 |
0.0014 |
| 1.2 |
0.44 |
|
2.45 |
0.18 |
|
10.0 |
0.001 |
Let us see how this table can be used to find the activity remaining after some elapsed time. Assume you have 100
mCi of a radioactive nuclide with a half-life of 6 hours. How much activity will remain after 33 hours? The first step is to express the elapsed time in terms of half-lives:
n = 33 hr/6 hr = 5.5.
The remaining fraction is
f = (0.5)5.5 .
The value of this is obtained from the table above and is
f = 0.022 (2.2%).
Therefore, if we started with 100 mCi, 2.2
mCi would remain after an elapsed time of 33 hours.
Another expression relating remaining fraction to elapsed time is
f = e-lt
where l
is the transformation constant and t is the elapsed time expressed in the same time units (hours, days, etc.) as the transformation constant. To determine the remaining fraction from this expression also requires a calculator that can perform exponential functions or special exponential tables.
|
|
|
CONTENTS |
|
We have considered fixed quantities of radioactive material that decay with elapsed time. If the radioactive material is being formed or replenished during the decay process, however, the relationship between activity and elapsed time is quite different from a simple exponential decay. The form of this relationship depends on the relationship of the rate of formation to the rate of decay. If we began by forming radioactive material, we would expect the activity to increase with elapsed time as illustrated
below. As the amount of radioactive material (and activity) increases, however, the rate of loss of material by radioactive transitions also increases.
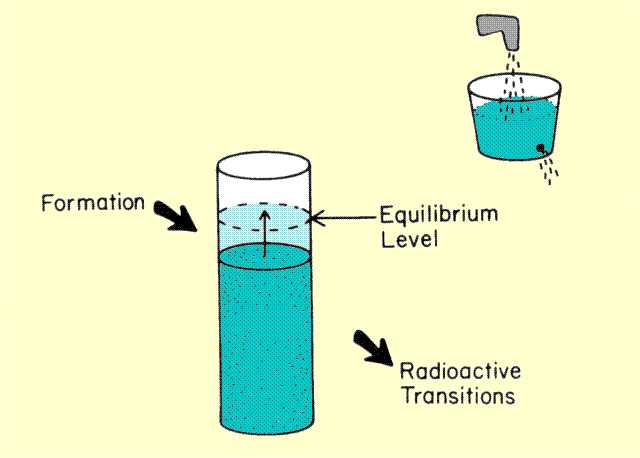
Concept of Equilibrium
Consider filling a bucket with a hole in it. As the water level rises in the bucket, the rate at which water flows out of the hole also increases. The water will usually reach a level at which the rate of loss is equal to the rate of filling, and the water level will remain constant. This could be described as a state of equilibrium between the rate of filling and rate of loss. The same process occurs with radioactive material. As the amount of material or activity builds up, the rate of loss by radioactive transitions can, under certain conditions, become the same as the rate of formation, and a state of equilibrium will be established. When the radioactive material being formed is the daughter of a radioactive parent, as illustrated
below, the type of activity-time relationship depends on the relationship of the two half-lives. If the half-life of the parent is shorter, no state of equilibrium will be reached. If the half-life of the parent is longer, and long enough that there is no noticeable decay during the time interval of interest, a condition of secular equilibrium will be reached. If the parent half-life is longer, but short enough so that there is a noticeable decay of the parent during the time interval of interest, a condition of transient equilibrium will be reached.
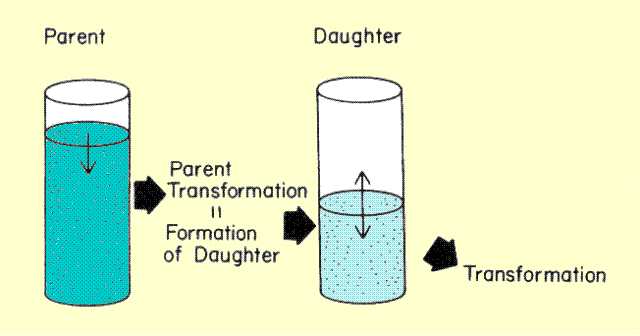
Factors Affecting Build-up of Daughter Activity
When a state of equilibrium is reached, the activity of the radioactive daughter is determined by the activity of the parent.
|
|
|
|
|
CONTENTS |
|
Assume that the radioactive material is forming at an almost constant rate. If, at the beginning, no radioactive daughter material is present, no nuclei will be under going transition. As soon as the radioactive material begins to accumulate, transitions will begin and some radioactive nuclei will be lost. As the number of radio active nuclei increases, the activity and rate of loss increase. Initially, the rate of loss is much less than the rate of formation. As the quantity of radioactive material builds, the activity or transition rate increases until it is equal to the rate of formation as shown
below. In other words, radioactive nuclei undergo transitions at exactly the same rate they are forming, and a condition of equilibrium is established. The amount of radioactive material will then remain constant regardless of elapsed time. Under this condition, the activity is equal to the rate of formation and is referred to as the saturation activity. The important point is that the maximum activity of a radioactive material is determined by the rate (nuclei per second) at which the material is being formed. Although it is true that the activity gradually builds with time, a point is reached at which build-up stops and the activity remains at the saturation level.
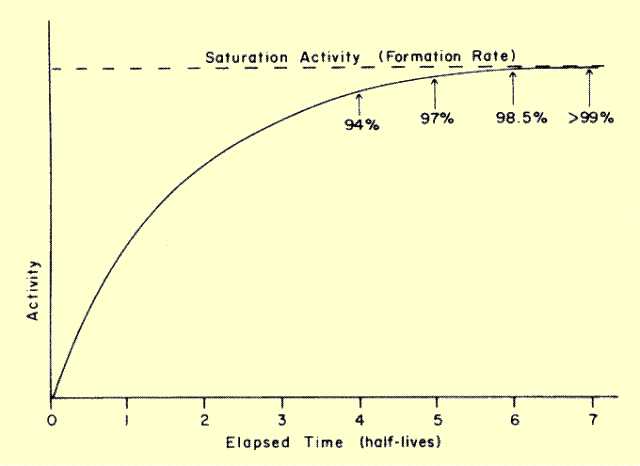
Build-up of Activity to Saturation Level during Transient Equilibrium
The time required to reach a specific activity depends on the half-life of the material being formed (daughter). After n half-lives the activity will be some fraction, f, of the rate of formation or saturation activity. The relationship is
f = 1 - (1/2)n.
Activity values after a specific elapsed time can be obtained for this relationship by using Table 6-1 to find the value of
(1/2)n. It should be observed that the build up of radioactivity is a mirror image of radioactive decay. Just as a radioactive material never decays to zero activity (at least theoretically), radioactive build-up never reaches saturation. However, for practical purposes, saturation is reached in approximately five half-lives when the activity is more than 96% of the saturation value.
After the activity reaches the saturation value it remains constant and is in a state of secular equilibrium. This occurs when the rate of formation does not change during the time period of interest because either the parent material has a very long half-life or the radioactive material is forming at a constant rate by another means such as a cyclotron or nuclear reactor.
|
|
|
|
CONTENTS |
|
When the half-life of the parent is only a few times greater than the half-life of the daughter, the condition of transient equilibrium will occur. During the period of interest the parent will undergo radioactive decay. Daughter activity will build and establish a state of equilibrium with the parent activity. Transient equilibrium differs from secular equilibrium in two respects.
First, the equilibrium or saturation activity of the daughter,
Ad, is not equal to the activity of the parent,
Ap. The relationship is
Ad
= Ap
Tp/(Tp
- Td).
When the half-life of the parent, Tp, is much greater than that of the daughter,
Td, the term
(Tp/Tp-Td) approaches a value of one, and daughter activity approaches parent activity, as in secular equilibrium. However, as daughter and parent half-lives become closer, this term becomes greater than one, which means that daughter activity is actually greater than parent activity under equilibrium conditions. The ratio of daughter to parent activity becomes greater as the half-lives become closer.
Second, with transient equilibrium the equilibrium activity of the daughter changes with time because the parent activity is changing. The relationship of parent and daughter activity for a transient condition is shown
below. After the condition of equilibrium is reached, the daughter appears to decay with the half-life of the parent.
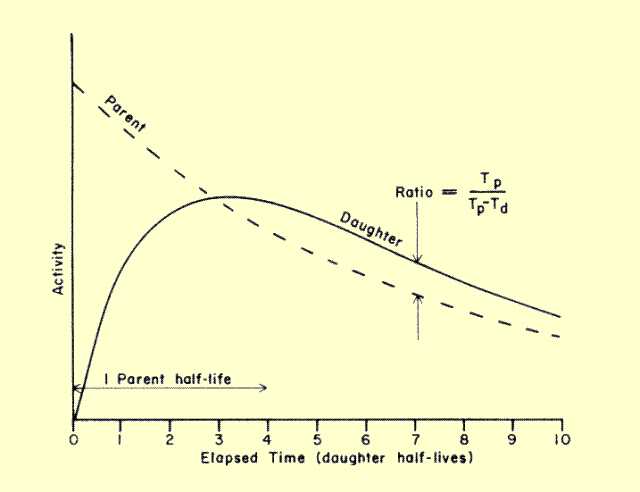
Transient Equilibrium
Molybdenum and Technetium Activity in a Generator
Technetium-99m and molybdenum-99 are good examples of transient equilibrium. Technetium-99m is obtained from a generator that contains molybdenum 99. The molybdenum-99 undergoes an isobaric transition into technetium-99m (86%) and technetium-99 (14%). The technetium-99m is radioactive with a half-life of 6 hours. Molybdenum-99 has a half-life of approximately 67 hours. The relationship between technetium and molybdenum activity in a typical generator is shown
below. In this example it is assumed that all technetium is removed from the generator every 24 hours.

Molybdenum and Technetium Activity in a Generator
If all molybdenum nuclei changed into technetium-99m nuclei, the saturation activity would be
ATc =
Amo
Tmo /
(Tmo-
TTc)
= 67/61 Amo
=1.1 Amo.
However, since only about 86% of the molybdenum-99 goes to technetium-99m, the saturation activity of technetium-99m will be only about 95% of the molybdenum-99 activity. In a 24-hour period (4 half-lives), the activity of technetium 99m will be approximately 94% of the saturation activity value. This would be only 84% of the molybdenum activity at that particular time.
|
|
|
|
CONTENTS |
|
When a radioactive material is in a living organism, the material can be re moved from a particular organ or location by two mechanisms, as illustrated
below. One is the normal radioactive decay, and the other is biological transport or elimination from the specific site.
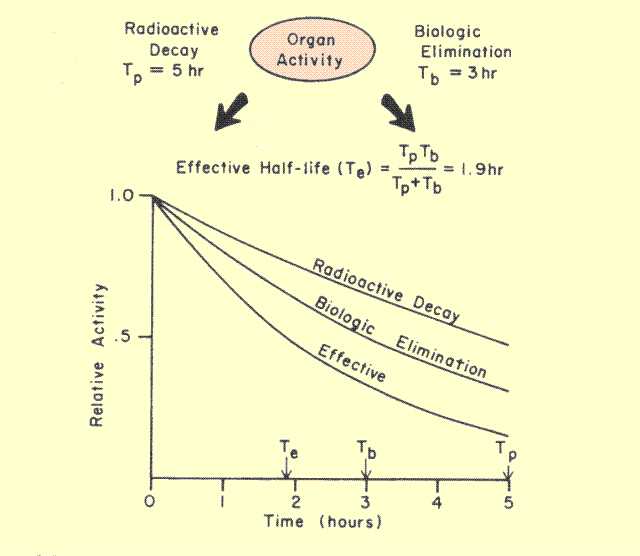
Relationship of Effective Lifetime to Rates of Radioactive Decay and Biological Elimination
Half-life values can be used to express the rate of removal by both mechanisms. The half-life associated with normal radioactive decay is generally designated the physical half-life and has a characteristic value for each radionuclide. The rate of biological removal can generally be expressed in terms of the biological half-life. The value of the biological half-life is determined by such things as the chemical form of the radionuclide and the physiological function of the organ or organism considered.
When biological transport or elimination occurs, the lifetime of the radioactive material in the organ is reduced. This is generally expressed in terms of an effective half-life. The relationship between effective half-life
(Te), physical half-life
(Tp), and biological half-life
(Tb) is given by
Te =
(Tp x
Tb)
/ ( Tp+Tb)
When both radioactive decay and biological elimination are present, the effective half-life will always be less than either the physical or biological half-life. If the difference in the two half-life values is rather large, the effective half-life will be slightly less than the shorter half-life of the two; if the two are equal, the effective half-life will be one-half of the physical or biological half-life value.
|
|
| |