|
|
|
CONTENTS |
|
X-ray photons are created by the interaction of energetic electrons with matter at the atomic level. Photons (x-ray and gamma) end their lives by transferring their energy to electrons contained in matter. X-ray interactions are important in diagnostic examinations for many reasons. For example, the selective interaction of x-ray photons with the structure of the human body produces the image; the interaction of photons with the receptor converts an x-ray or gamma image into one that can be viewed or recorded. This chapter considers the basic interactions between x-ray and gamma photons and matter.
|
|
|
|
CONTENTS |
|
Recall that photons are individual units of energy. As an x-ray beam or gamma radiation passes through an object, three possible fates await each photon, as shown in
the figure below:
1. It can
penetrate the section of matter without interacting.
2. It can interact with the matter and be
completely absorbed by depositing its energy.
3. It can interact and be
scattered or deflected from its original direction and deposit part of its energy.
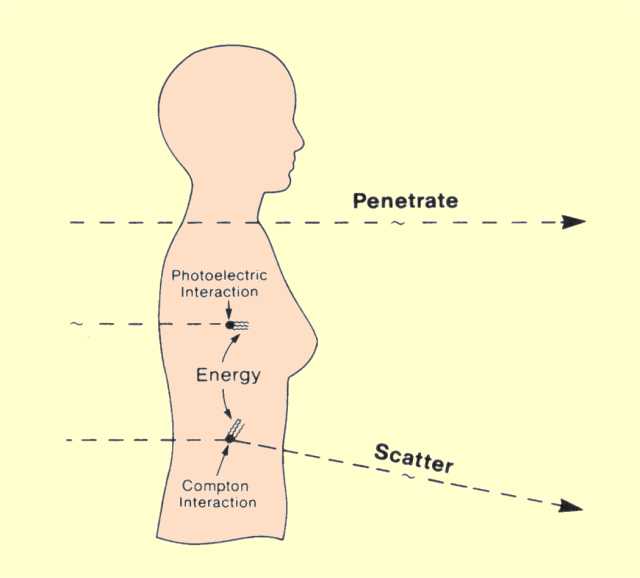
Photons Entering the Human Body Will Either Penetrate, Be Absorbed, or Produce Scattered Radiation
There are two kinds of interactions through which photons deposit their energy; both are with electrons. In one type of interaction the photon loses all its energy; in the other, it loses a portion of its energy, and the remaining energy is scattered. These two interactions are shown
below.
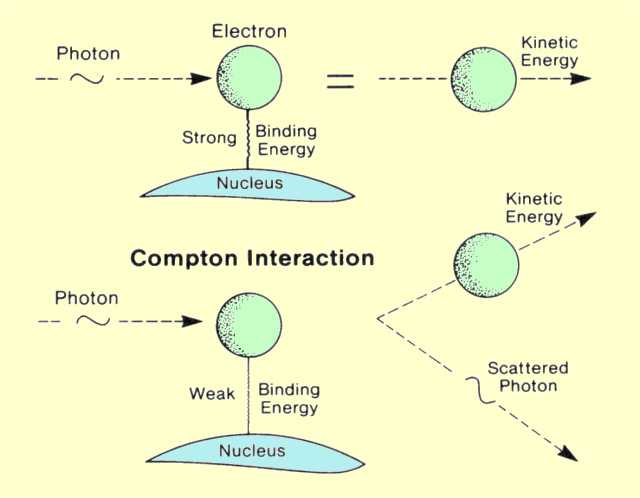
The Two Basic Interactions Between Photons and Electrons
|
|
|
|
CONTENTS |
|
In the photoelectric (photon-electron) interaction, as shown above, a photon transfers all its energy to an electron located in one of the atomic shells. The electron is ejected from the atom by this energy and begins to pass through the surrounding matter. The electron rapidly loses its energy and moves only a relatively short distance from its original location. The photon's energy is, therefore, deposited in the matter close to the site of the photoelectric interaction. The energy transfer is a two-step process. The photoelectric interaction in which the photon transfers its energy to the electron is the first step. The depositing of the energy in the surrounding matter by the electron is the second step.
Photoelectric interactions usually occur with electrons that are firmly bound to the atom, that is, those with a relatively high binding energy. Photoelectric interactions are most probable when the electron binding energy is only slightly less than the energy of the photon. If the binding energy is more than the energy of the photon, a photoelectric interaction cannot occur. This interaction is possible only when the photon has sufficient energy to overcome the binding energy and remove the electron from the atom.
The photon's energy is divided into two parts by the interaction. A portion of the energy is used to overcome the electron's binding energy and to remove it from the atom. The remaining energy is transferred to the electron as kinetic energy and is deposited near the interaction site. Since the interaction creates a vacancy in one of the electron shells, typically the K or L, an electron moves down to fill in. The drop in energy of the filling electron often produces a characteristic x-ray photon. The energy of the characteristic radiation depends on the binding energy of the electrons involved. Characteristic radiation initiated by an incoming photon is referred to as fluorescent radiation. Fluorescence, in general, is a process in which some of the
energy of a photon is used to create a second photon of less energy. This process sometimes converts x-rays into light photons. Whether the fluorescent radiation is in the form of light or x-rays depends on the binding energy levels in the absorbing material.
|
|
|
|
CONTENTS |
|
A Compton interaction is one in which only a portion of the energy is absorbed and a photon is produced with reduced energy. This photon leaves the site of the interaction in a direction different from that of the original photon, as shown in
the previous figure. Because of the change in photon direction, this type of interaction is classified as a scattering process. In effect, a portion of the incident radiation "bounces off' or is scattered by the material. This is significant in some situations because the material within the primary x-ray beam becomes a secondary radiation source. The most significant object producing scattered radiation in an x-ray procedure is the patient's body. The portion of the patient's body that is within the primary x-ray beam becomes the actual source of scattered radiation. This has two undesirable consequences. The scattered radiation that continues in the forward . direction and reaches the image receptor decreases the quality (contrast) of the image; the radiation that is scattered from the patient is the predominant source of radiation exposure to the personnel conducting the examination.
|
|
|
|
CONTENTS |
|
There are actually two types of interactions that produce scattered radiation. One type, referred to by a variety of names, including coherent, Thompson,
Rayleigh, classical, and elastic, is a pure scattering interaction and deposits no energy in the material. Although this type of interaction is possible at low photon energies, it is generally not significant in most diagnostic procedures.
|
|
|
|
CONTENTS |
|
Pair production is a photon-matter interaction that is not encountered in diagnostic procedures because it can occur only with photons with energies in excess of 1.02
MeV. In a pair-production interaction, the photon interacts with the nucleus in such a manner that its energy is converted into matter. The interaction produces a pair of particles, an electron and a positively charged positron. These two particles have the same mass, each equivalent to a rest mass energy of 0.51
MeV.
|
|
|
|
CONTENTS |
|
The interaction and transfer of energy from photons to tissue has two phases. The first is the "one-shot" interaction between the photon and an electron in which all or a significant part of the photon energy is transferred; the second is the transfer of energy from the energized electron as it moves through the tissue. This occurs as a series of interactions, each of which transfers a relatively small amount of energy.
Several types of radioactive transitions produce electron radiation including beta radiation, internal conversion (IC) electrons, and Auger electrons. These radiation electrons interact with matter (tissue) in a manner similar to that of electrons produced by photon interactions.
In photoelectric interactions, the energy of the electron is equal to the energy of the incident photon less the binding energy of the electron within the atom. In Compton interactions, the relationship of the electron energy to that of the photon depends on the angle of scatter and the original photon energy. The electrons set free by these interactions have kinetic energies ranging from relatively low values to values slightly below the energy of the incident photons.
As the electrons leave the interaction site, they immediately begin to transfer their energy to the surrounding material, as shown
below. Because the electron carries an electrical charge, it can interact with other electrons without touching them. As it passes through the material, the electron, in effect, pushes the other electrons away from its path. If the force on an electron is sufficient to remove it from its atom, ionization results. In some cases, the atomic or molecular structures are raised to a higher energy level, or excited state. Regardless of the type of interaction, the moving electron loses some of its energy. Most of the ionization produced by x- and gamma radiation is not a result of direct photon interactions, but rather of interactions of the energetic electrons with the material. For example, in air, radiation must expend an average energy of 33.4 eV per ionization. Consider a 50-keV x-ray photon undergoing a photoelectric interaction. The initial interaction of the photon ionizes one atom, but the resulting energetic electron ionizes approximately 1,500 additional atoms.
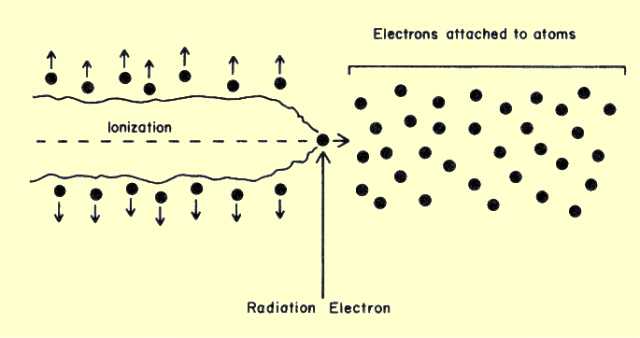
Ionization Produced by a Radiation Electron
|
|
|
|
CONTENTS |
|
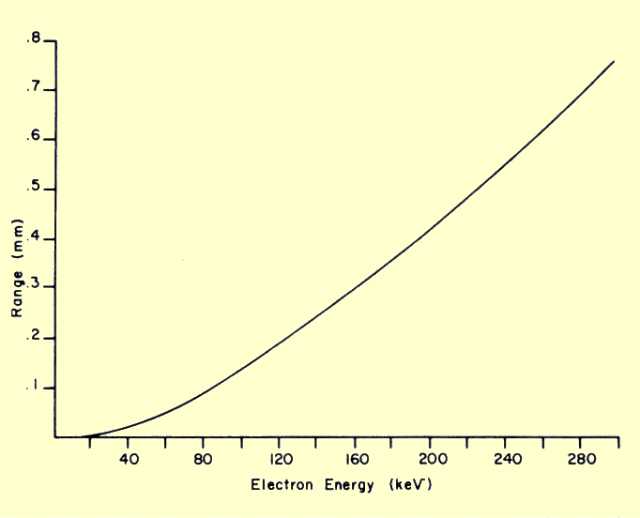
The total distance an electron travels in a material before losing all its energy is generally referred to as its range. The two factors that determine the range are (1) the initial energy of the electrons and (2) the density of the material. One important characteristic of electron interactions is that all electrons of the same energy have the same range in a specific material, as illustrated
immediately below. The general relationship between electron range and energy is shown in
the second following figure. The curve shown is the range for a material with a density of 1 g/cm3. This is the density of water and the approximate density of muscle tissue.
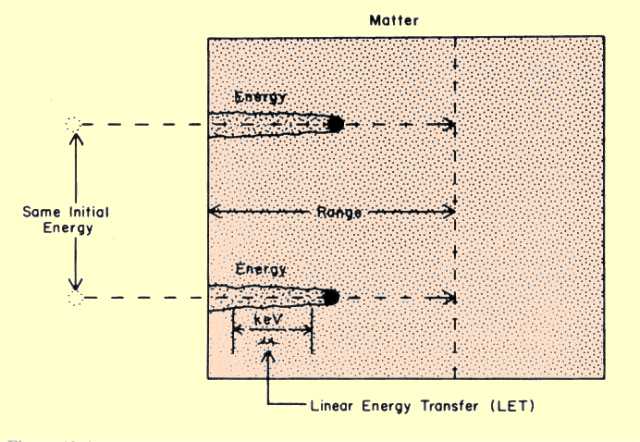
The Range of Electrons with the Same Initial Energies
Relationship of Electron Range to Initial Energy in a Material with a Density of 1
g/cm3 (Soft Tissue)
The electron range in other materials can be determined by dividing the range given in
the figure above by the density of the material. Let us now apply this procedure to determine the range of 300-keV beta particles in air. (Air has a density of 0.00129
g/cm3.) From
the figure we see that a 300-keV electron has a range of 0.76 mm in a material with a density of 1
g/cm3. When this value is divided by the density of air, we find the range to be 59 cm.
In general, the range of electron radiation in materials such as tissue is a fraction of a millimeter. This means that essentially all electron radiation energy is absorbed in the body very close to the site containing the radioactive material.
|
|
|
|
CONTENTS |
|
The rate at which an electron transfers energy to a material is known as the linear energy transfer (LET), and is expressed in terms of the amount of energy transferred per unit of distance traveled. Typical units are kiloelectron volts per micrometer (keV/um). In a given material, such as tissue, the LET value depends on the kinetic energy (velocity) of the electron. The LET is generally inversely related to the electron velocity. As a radiation electron loses energy, its velocity decreases, and the value of the LET increases until all its energy is dissipated. LET values in soft tissue for several electron energies are given below.
Electron Energy vs. Linear
Energy Transfer
| Electron Energy (keV) |
LET (keV / mm) |
| 1000 |
0.2 |
| 100 |
0.3 |
| 10 |
2.2 |
| 1 |
12.0 |
The effectiveness of a particular radiation in producing biological damage is often related to the LET of the radiation. The actual relationship of the efficiency in producing damage to LET values depends on the biological effect considered. For some effects, the efficiency increases with an increase in LET, for some it decreases, and for others it increases up to a point and then decreases with additional increases in LET. For a given biological effect, there is an LET value that produces an optimum energy concentration within the tissue. Radiation with lower LET values does not produce an adequate concentration of energy. Radiations with higher LET values tend to deposit more energy than is needed to produce the effect; this tends to waste energy and decrease efficiency.
|
|
|
|
CONTENTS |
|
Recall that a positron is the same size as an electron, but has a positive charge. It is also different from the electron in that it is composed of what is referred to as antimatter. This leads to a type of interaction that is quite different from the interactions among electrons.
The interaction between a positron and matter is in two phases, as illustrated
below. These are ionization and annihilation. As the energetic positron passes through matter, it interacts with the atomic electrons by electrical attraction. As the positron moves along, it pulls electrons out of the atoms and produces ionization. A small amount of energy is lost by the positron in each interaction. In general, this phase of the interaction is not too unlike the interaction of an energetic electron, but the positron pulls electrons as it races by and electrons push electrons away-from the path. Also, when the positron has lost most of its kinetic energy and is coming to a stop, it comes into close contact with an electron and enters into an annihilation interaction.
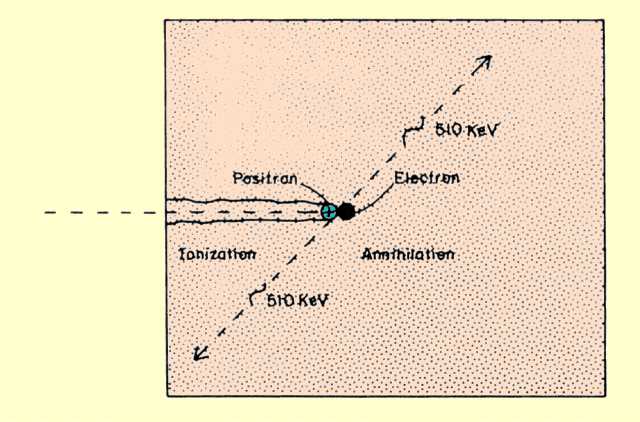
A Positron Interaction That Produces Annihilation Radiation
The annihilation process occurs when the antimatter positron combines with the conventional-matter electron. In this interaction, the masses of both particles are completely converted into energy. The relationship between the amount of energy and mass is given by
E= mc2.
The energy equivalent of one electron or positron mass is 511 keV. The energy that results from the annihilation process is emitted from the interaction site in the form of two photons, each with an energy of 511 keV. The pair of photons leave the site in opposite directions. With special imaging equipment it is possible to capture both photons and to determine the precise three-dimensional location of the interaction site. Since the range of a positron, like that of an electron, is relatively short, the site of interaction is always very close to the location of the radioactive nuclei.
|
|
|
|
CONTENTS |
|
As a photon makes its way through matter, there is no way to predict precisely either how far it will travel before engaging in an interaction or the type of interaction it will engage in. In clinical applications we are generally not concerned with the fate of an individual photon but rather with the collective interaction of the large number of photons. In most instances we are interested in the overall rate at which photons interact as they make their way through a specific material.
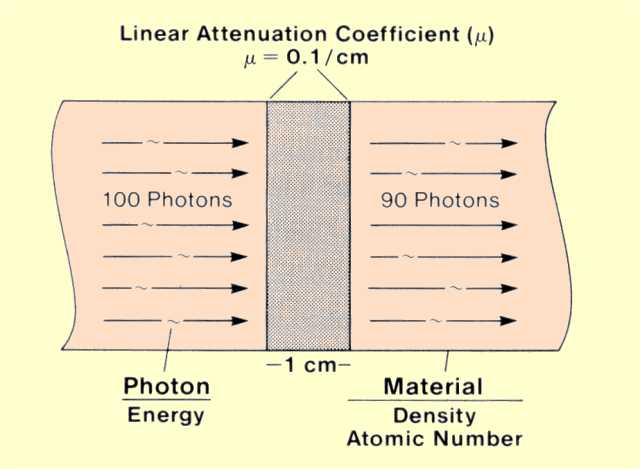
Let us observe what happens when a group of photons encounters a slice of material that is 1 unit thick, as illustrated
in the figure below. Some of the photons interact with the material, and some pass on through. The interactions, either photoelectric or Compton, remove some of the photons from the beam in a process known as attenuation. Under specific conditions, a certain percentage of the photons will interact, or be attenuated, in a 1-unit thickness of material.
Linear Attenuation Coefficient
|
|
|
|
CONTENTS |
The linear attenuation coefficient (µ) is the actual fraction of photons interacting per 1-unit thickness of material. In our example the fraction that interacts in the 1-cm thickness is 0.1, or 10%, and the value of the linear attenuation coefficient is 0.1 per cm.
Linear attenuation coefficient values indicate the rate at which photons interact as they move through material and are inversely related to the average distance photons travel before interacting. The rate at which photons interact (attenuation coefficient value) is determined by the energy of the individual photons and the atomic number and density of the material.
|
|
|
|
CONTENTS |
|
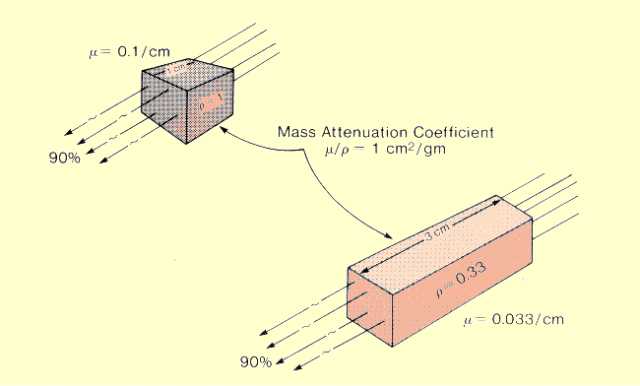
In some situations it is more desirable to express the attenuation rate in terms of the mass of the material encountered by the photons rather than in terms of distance. The quantity that affects attenuation rate is not the total mass of an object but rather the area mass. Area mass is the amount of material behind a 1-unit surface area, as shown
below. The area mass is the product of material thickness and density:
Area Mass (g/cm2) = Thickness (cm)
x
Density
(g/cm3).
The mass attenuation coefficient is the rate of photon interactions per 1-unit (g/cm2) area mass.
Mass Attenuation Coefficient
The figure compares two pieces of material with different thicknesses and densities but the same area mass. Since both attenuate the same fraction of photons, the mass attenuation coefficient is the same for the two materials. They do not have the same linear attenuation coefficient values.
The relationship between the mass and linear attenuation coefficients is
Mass Attenuation Coefficient (µ/r) =
Linear Attenuation Coefficient (µ)
/ Density (r).
Notice that the symbol for mass attenuation coefficient (µ/r) is derived from the symbols for the linear attenuation coefficient (µ) and the symbol for density
(r). We must be careful not to be misled by the relationship stated in this manner. Confusion often arises as to the effect of material density on attenuation coefficient values. Mass attenuation coefficient values are actually normalized with respect to material density, and therefore do not change with changes in density. Material density does have a direct effect on linear attenuation coefficient values.
The total attenuation rate depends on the individual rates associated with photoelectric and Compton interactions. The respective attenuation coefficients are related as follows:
µ(total) = µ(photoelectric) + µ(Compton).
Let us now consider the factors that affect attenuation rates and the competition between photoelectric and Compton interactions. Both types of interactions occur with electrons within the material. The chance that a photon will interact as it travels a 1-unit distance depends on two factors.
One factor is the concentration, or density, of electrons in the material. Increasing the concentration of electrons increases the chance of a photon coming close enough to an electron to interact. In
a previous section (Characteristics and Structure of Matter) we observed that electron concentration was determined by the physical density of the material. Therefore, density affects the probability of both photoelectric and Compton interactions.
All electrons are not equally attractive to a photon. What makes an electron more or less attractive is its binding energy. The two general rules are:
1. Photoelectric interactions occur most frequently when the electron binding energy is slightly less than the photon energy.
2. Compton interactions occur most frequently with electrons with relatively low binding energies.
In the previous section referred to above we observed that the electrons with binding energies within the energy range of diagnostic x-ray photons were the K-shell electrons of the intermediate- and high-atomic-number materials. Since an atom can have, at the most, two electrons in the K shell, the majority of the electrons are located in the other shells and have relatively low binding energies.
|
|
|
|
CONTENTS |
|
The probability, and thus attenuation coefficient value, for photoelectric interactions depends on how well the photon energies and electron binding energies match, as shown
below. This can be considered from two perspectives.
In a specific material with a fixed binding energy, a change in photon energy alters the match and the chance for photoelectric interactions. On the other hand, with photons of a specific energy, the probability of photoelectric interactions is affected by the atomic number of the material, which changes the binding energy.
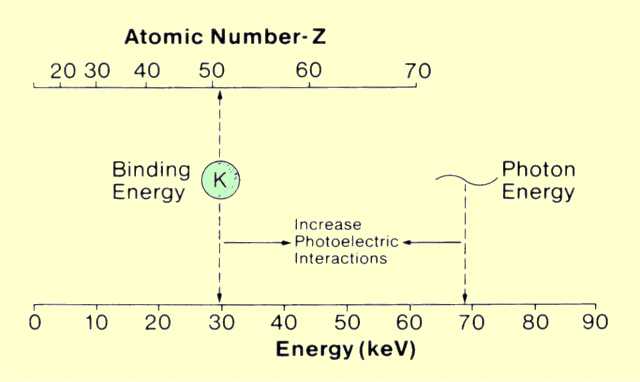
The Relationship between Material Atomic Number and Photon Energy That Enhances the Probability of Photoelectric Interactions
|
|
|
|
CONTENTS |
|
In a given material, the probability of photoelectric interactions occurring is strongly dependent on the energy of the photon and its relationship to the binding energy of the electrons.
The figure below shows the relationship between the attenuation coefficient for iodine (Z = 53) and photon energy. This graph shows two significant features of the relationship. One is that the coefficient value, or the probability of photoelectric interactions, decreases rapidly with increased photon energy. It is generally said that the probability of photoelectric interactions is inversely proportional to the cube of the photon energy
(1/E3). This general relationship can be used to compare the photoelectric attenuation coefficients at two
different photon energies. The significant point is that the probability of photoelectric interactions occurring in a given material drops drastically as the photon energy is increased.
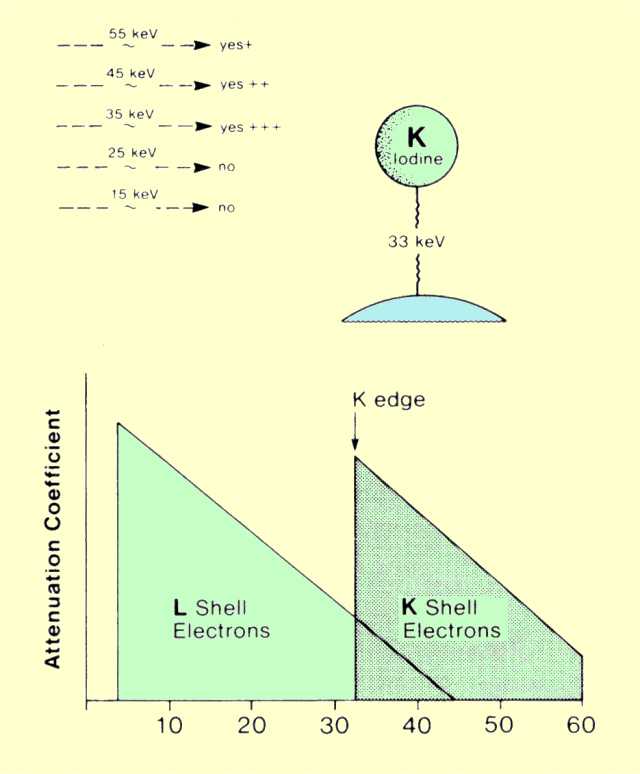
Relationship between the Probability of Photoelectric Interactions and Photon Energy
The other important feature of the attenuation coefficient-photon energy relationship shown in
the figure above is that it changes abruptly at one particular energy: the binding energy of the shell electrons. The K-electron binding energy is 33 keV for iodine. This feature of the attenuation coefficient curve is generally designated as the K, L, or M edge. The reason for the sudden change is apparent if it is recalled that photons must have energies equal to or slightly greater than the binding energy of the electrons with which they interact. When photons with energies less than 33 keV pass through iodine, they interact primarily with the L-shell electrons. They do not have sufficient energy to eject electrons from the K shell, and the probability of interacting with the M and N shells is quite low because of the relatively large difference between the electron-binding and photon energies. However, photons with energies slightly greater than 33 keV can also interact with the K shell electrons. This means that there are now more electrons in the material that are available for interactions. This produces a sudden increase in the attenuation coefficient at the K-shell energy. In the case of iodine, the attenuation coefficient abruptly jumps from a value of 5.6 below the K edge to a value of 36, or increases by a factor of more than 6.
A similar change in the attenuation coefficient occurs at the L-shell electron binding energy. For most elements, however, this is below 10 keV and not within the useful portion of the x-ray spectrum.
Photoelectric interactions occur at the highest rate when the energy of the x-ray photon is just above the binding energy of the electrons.
|
|
|
|
CONTENTS |
|
The probability of photoelectric interactions occurring is also dependent on the atomic number of the material. An explanation for the increase in photoelectric interactions with atomic number is that as atomic number is increased, the binding energies move closer to the photon energy. The general relationship is that the probability of photoelectric interactions (attenuation coefficient value) is proportional to Z3. In general, the conditions that increase the probability of photoelectric interactions are low photon energies and high-atomic-number materials.
|
|
|
|
CONTENTS |
|
Compton interactions can occur with the very loosely bound electrons. All electrons in low-atomic-number materials and the majority of electrons in high-atomic-number materials are in this category. The characteristic of the material that affects the probability of Compton interactions is the number of available electrons. It was shown earlier that all materials, with the exception of hydrogen, have approximately the same number of electrons per gram of material. Since the concentration of electrons in a given volume is proportional to the density of the materials, the probability of Compton interactions is proportional only to the physical density and not to the atomic number, as in the case of photoelectric interactions. The major exception is in materials with a significant proportion of hydrogen. In these materials with more electrons per gram, the probability of Compton interactions is enhanced.
Although the chances of Compton interactions decrease slightly with photon energy, the change is not so rapid as for photoelectric interactions, which are inversely related to the cube of the photon energy.
|
|
|
|
CONTENTS |
|
It is possible for photons to scatter in any direction. The direction in which an individual photon will scatter is purely a matter of chance. There is no way in which the angle of scatter for a specific photon can be predicted. However, there are certain directions that are more probable and that will occur with a greater frequency than others. The factor that can alter the overall scatter direction pattern is the energy of the original photon. In diagnostic examinations, the most significant scatter will be in the forward direction. This would be an angle of scatter of only a few degrees. However, especially at the lower end of the energy spectrum, there is a significant amount of scatter in the reverse direction,
i.e., backscatter. For the diagnostic photon energy range, the number of photons that scatter at right angles to the primary beam is in the range of one-third to one-half of the number that scatter in the forward direction. Increasing primary photon energy causes a general shift of scatter to the forward direction. However, in diagnostic procedures, there is always a significant amount of back- and
side-scatter radiation.
|
|
|
|
CONTENTS |
|
When a photon undergoes a Compton interaction, its energy is divided between the scattered secondary photon and the electron with which it interacts. The electron's kinetic energy is quickly absorbed by the material along its path. In other words, in a Compton interaction, part of the original photon's energy is absorbed and part is converted into scattered radiation.
The manner in which the energy is divided between scattered and absorbed radiation depends on two factors-the angle of scatter and the energy of the original photon. The relationship between the energy of the scattered radiation and the angle of scatter is a little complex and should be considered in two steps. The photon characteristic that is specifically related to a given scatter angle is its change in wavelength. It should be recalled that a photon's wavelength
(l) and energy
(E) are inversely related as given by:
E = 12.4 / l.
Since photons lose energy in a Compton interaction, the wavelength always increases. The relationship between the change in a photon's wavelength,
Dl, and the angle of scatter is given by:
Dl =
0.024 (1 - cos q).
For example, all photons scattered at an angle of 90 degrees, where the cosine has a value of 0, will undergo a wavelength change of 0.024 Å. Photons that scatter back at an angle of 180 degrees where the cosine has a value of -1 will undergo a wavelength change of 0.048 Å. This is the maximum wavelength change that can occur in a scattering interaction.
It is important to recognize the difference between a change in wavelength and a change in energy. Since higher energy photons have shorter wavelengths, a change of say 0.024 Å represents a larger energy change than it would for a lower energy photon. All photons scattered at an angle of 90 degrees will undergo a wavelength change of 0.0243Å The change in energy associated with 90-degree scatter is not the same for all photons and depends on their original energy. The change in energy can be found as follows. For a 110-keV photon, the wavelength is 0.1127 Å. A scatter angle of 90 degrees will always increase the wavelength by 0.0243. Therefore, the wavelength of the scattered photon will be 0.1127 plus 0.0243 or 0.1370. The energy of a photon with this wavelength is 91 keV. The 110 keV photons will lose 19 keV or 17% of their energy in the scattering process. Lower energy photons lose a smaller percentage of their energy.
|
|
|
|
CONTENTS |
|
As photons pass through matter, they can engage in either photoelectric or Compton interactions with the material electrons. The photoelectric interaction captures all photon energy and deposits it within the material, whereas the Compton interaction removes only a portion of the energy, and the remainder continues as scattered radiation. The combination of the two types of interactions produces the overall attenuation of the x-ray beam. We now consider the factors that determine which of the two interactions is most likely to occur in a given situation.
The energy at which interactions change from predominantly photoelectric to Compton is a function of the atomic number of the material.
The figure below shows this crossover energy for several different materials. At the lower photon energies, photoelectric interactions are much more predominant than Compton. Over most of the energy range, the probability of both decreases with increased energy. However, the decrease in photoelectric interactions is much greater. This is because the photoelectric rate changes in proportion to 1/E3, whereas Compton interactions are much less energy dependent. In soft tissue, the two lines cross at an energy of about 30 keV. At this energy, both photoelectric and Compton interactions occur in equal numbers. Below this energy, photoelectric interactions predominate. Above 30 keV, Compton interactions become the significant process of x-ray attenuation. As photon energy increases, two changes occur:
The probability of both types of interactions decreases, but the decrease for Compton is less, and it becomes the predominant type of interaction.
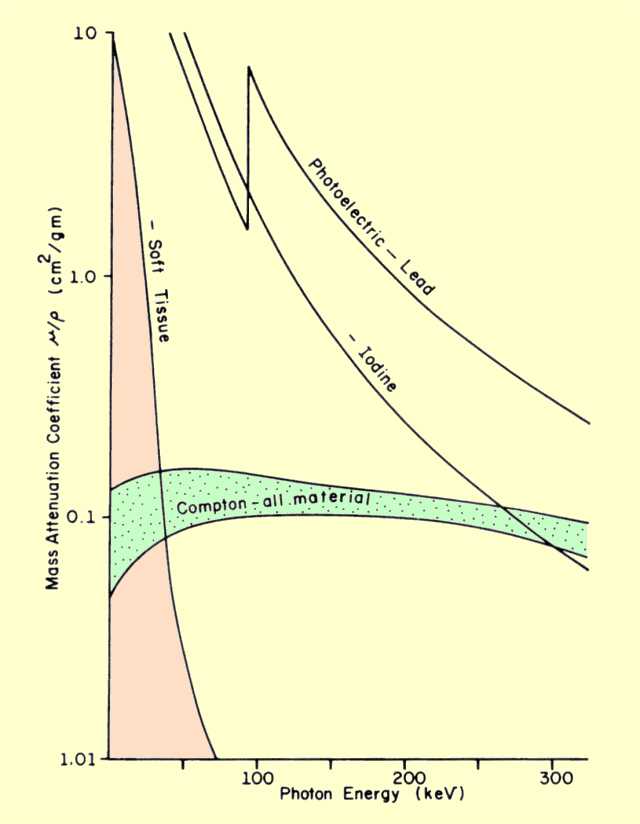
Comparison of Photoelectric and Compton Interaction Rates for Different Materials and Photon Energies
In higher-atomic-number materials, photoelectric interactions are more probable, in general, and they predominate up to higher photon energy levels. The conditions that cause photoelectric interactions to predominate over Compton are the same conditions that enhance photoelectric interactions, that is, low photon energies and materials with high atomic numbers.
The total attenuation coefficient value for materials involved in x-ray and gamma interactions can vary tremendously if photoelectric interactions are involved. A minimum value of approximately 0.15
cm2/g is established by Compton interactions. Photoelectric interactions can cause the total attenuation to increase to very high values. For example, at 30 keV, lead (Z = 82) has a mass attenuation coefficient of 30
cm2/g.
|
|
|